2023-2024学年人教版初中数学九年级下册27.2.3 相似三角形应用举例 同步分层训练基础题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm，6cm和9cm，另一个三角形的最短边长为2.5cm，则它的最长边长为（ ）．A、3cm B、4cm C、4.5cm D、5cm2. 如图，在平行四边形中，点E在边上， ， 连接交于点F，则的面积与的面积之比为（ ）
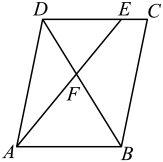A、 B、 C、 D、3. 如图，它是物理学中小孔成像的原理示意图，已知物体 ， 根据图中尺寸 ， 则的长应是（ ）
A、15 B、30 C、20 D、104. 如图所示，树AB在路灯的照射下形成投影AC，已知路灯高 ， 树影 ， 树AB与路灯的水平距离 ， 则树的高度AB是（ ）.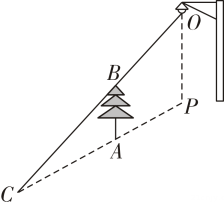
A、2m B、3m C、 D、5. 如图，阳光从教室的窗户射入室内，窗户框AB在地面上的影子长DE＝1.8m，窗户下沿到地面的距离BC＝1m，EC＝1.2m，那么窗户的高AB为（ ）
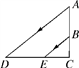A、1.5m B、1.6m C、1.86m D、2.16m6. 如图，路灯距离地面8米，若身高1.6米的小明在距离路灯的底部（点O）20米的A处，则小明的影子AM的长为（ ）
A、1.25米 B、5米 C、6米 D、4米7. 如图，小明设计的用激光笔测量城墙高度的示意图，在点处水平放置一面平面镜，光线从点A出发经平面镜反射后刚好射到城墙的顶端处，已知 ， ， 米，米，米，那么该城墙的高度为（ ）
A、6 B、8 C、10 D、188. 如图，一壁厚均匀的容器外径为 ， 用一个交叉卡钳（两条尺长和相等）可测量容器的内部直径．如果 ， 且量得 ， 则零件的厚度x为（ ）
A、 B、 C、 D、二、填空题
-
9. 如图，某学生利用一根长1米的标杆测量一棵树的高度，测得米，米，那么树的高度为米.
10. 如图是小孔成像原理的示意图， ， ， . 若物体的高度为 ， 则像的高度是.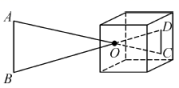
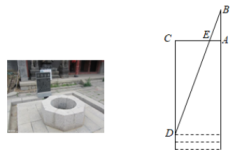
11. 据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验，阐释了光的直线传播原理，如图（1）所示。如图（2）所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是cm．
12. 《九章算术》中记载了一种测量古井水面以上部分深度的方法．如图所示，在井口A处立一根垂直于井口的木杆 ， 从木杆的顶端B观察井水水岸D，视线与井口的直径交于点E，如果测得米，米，米，那么为米．
13. 如图，已知小丽的身高是1.6米，他在路灯下的影长为2米，小丽距路灯灯杆的底部3米，那么路灯灯泡距地面的高度是米．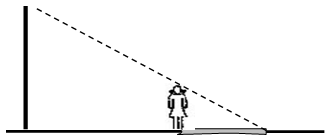
三、解答题
-
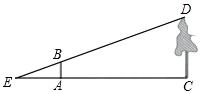
14. 如图，某学习小组为了测量校园内一棵小树的高度 ，用长为 的竹竿 作测量工具，移动竹竿，使竹竿影子的顶端、树影子的顶端落在水平地面上的同一点E，且点E，A，C在同一直线上.已知 ， ，求这棵树的高度 .
15. 如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度．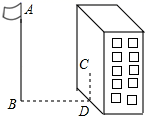
四、综合题
-
16. 如图，在锐角三角形中，为边的中点，为边所在的直线上一点，连接交延长线于 ， 已知 ， 问：
(1)、点此时的位置；(2)、求的值．17. 如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度DE＝3.5m，点F到地面的高度CF＝1.5m，灯泡到木板的水平距离AC＝5.4m，墙到木板的水平距离为CD＝4m．已知光在镜面反射中的入射角等于反射角，图中点A、B、C、D在同一水平面上．
(1)、求BC的长．(2)、求灯泡到地面的高度AG．