人教版数学九年级下册27.2.2相似三角形的性质同步分层训练培优题

试卷更新日期：2024-01-20 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，梯形ABCD中， $A B ∥ C D$ ，对角线AC、BD相交于点O，下面四个结论：① $△ A O B$ 与 $△ C O D$ 相似；② $△ A O D$ 与 $△ B O C$ 相似；③ $S_{△ D O C} ： S_{△ B O A} = D C ： A B$ ；④ $△ A O D$ 与 $△ B O C$ 面积相等.其中结论始终正确的有（）

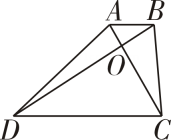A、①④ B、①③ C、①② D、②④

查看试题解析
2. 如图，正方形 $D E F G$ 的边 $E F$ 在 $△ A B C$ 的边 $B C$ 上，顶点D、G分别在边 $A B 、 A C$ 上，已知 $△ A B C$ 的边 $B C$ 长15厘米，高 $A H$ 为10厘米，则正方形 $D E F G$ 的边长是（）

A、4厘米 B、5厘米 C、6厘米 D、8厘米

查看试题解析
3. 如图，已知△ABC和△ADE均为等边三角形，点D在BC边上，DE与AC相交于点F，图中相似的三角形有（）对.

A、3 B、4 C、5 D、6

查看试题解析
4. 如图，在矩形 $A B C D$ 中，若 $A B = 6$ ， $A C = 10$ ， $\frac{E F}{B F} = \frac{3}{4}$ ，则 $A E$ 的长为（）

A、2 B、4 C、6 D、7.5

查看试题解析
5. 如图1，在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，D是AB上一点，且AD＝2，过点D作DE∥BC交AC于E ，将△ADE绕A点顺时针旋转到图2的位置．则图2中 $\frac{B D}{C E}$ 的值为（　　）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
6. 如图，平行四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O，E是 $C D$ 的中点，则 $△ D E O$ 与 $△ B C D$ 的面积的比等于（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
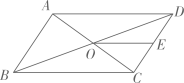7. 在等腰三角形ABC中，AB=AC，BC=6，内切圆的半径等于1，则腰长为（）

A、 $\frac{13}{4}$ B、4 C、 $\frac{15}{4}$ D、 $\frac{17}{4}$

查看试题解析
8. 如图，已知二次函数 $y = - \frac{5}{4} (x + 1) (x - 4)$ 的图象与x轴交于A、B两点（点A在点B的左侧），与 $y$ 轴交于点C，P为该二次函数在第一象限内的一点，连接AP，交BC于点K，则 $\frac{A P}{P K}$ 的最小值为（）

A、 $\frac{9}{4}$ B、2 C、 $\frac{7}{4}$ D、 $\frac{5}{4}$

查看试题解析

二、填空题

9. 如图， $△ A B C$ 和 $△ D E F$ 是以点 $O$ 为位似中心的位似图形，相似比为 $2$ ： $3$ ，则 $△ A B C$ 和 $△ D E F$ 的面积比是．

查看试题解析
10. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D$ 与 $A B$ 相交于点 $E$ ，若 $A E = 2$ ， $B E = 8$ ， $C E = 2 D E$ ，则 $O$ 到 $C D$ 的距离为.

查看试题解析
11. 如图，将正方形纸片进行如下操作：对折正方形ABCD得折痕EF，连接CE，将CB折叠到CE上，点B对应点H，得折痕CG，则 $\frac{A G}{B G}$ ＝．

查看试题解析
12. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 9 0^{\circ ，} A C = 3 B C = 6 B D = 2$ ，以点B为圆心，BD长为半径作圆，点E为⊙B上的动点，连结EC，作FC⊥CE，垂足为C，点F在直线BC的上方，且满足 $C F = \frac{1}{2} C E$ ，连结BF，当点E与点D重合时，BF的值为，点E在⊙B上运动过程中，BF存在最大值为．

查看试题解析
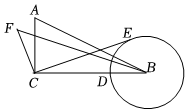13. 如图，正方形ABCD的边长为8，点E ， F分别是边BC ， CD上的动点，且BE＝CF ，连接AE ， BF交于点G ，点H为AG上一点，且BG＝GH ，连接DH ，则DH的最小值为．

查看试题解析

三、解答题

14. 如图，在 $▱ A B C D$ 中，点E在 $A B$ 上， $A E = \frac{1}{3} A B$ ， $E D$ 和 $A C$ 相交于点F，过点F作 $F G ∥ A B$ ，交 $A D$ 于点G．

(1)、求 $\frac{A F}{F C}$ 的值．

(2)、若 $A B ： A C = \sqrt{3} ： 2$ ，
①求证： $∠ A E F = ∠ A C B$ ．
②求证： $D F^{2} = D G \cdot D A$ ．

查看试题解析
15. 如图， $A B$ 为 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点， $D$ 为 $A B$ 上一点， $B D = B C$ ，过点 $A$ 作 $A E ⊥ A B$ 交 $C D$ 的延长线于点 $E$ ， $C E$ 交 $⊙ O$ 于点 $G$ ，连接 $A C$ ， $A G$ ，在 $E A$ 的延长线上取点 $F$ ，使 $∠ F C A = 2 ∠ E$ ．

(1)、求证： $C F$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为 $5$ ， $A C = 6$ ，求 $A G$ 的长．

查看试题解析

四、综合题

16. 如图 $1$ ，在正方形 $A B C D$ 中，点 $G$ 是对角线 $B D$ 上一点 $($ 不与点 $B$ ， $D$ 重合 $)$ ， $E G ⊥ B D$ 交边 $A B$ 于点 $E$ ，连接 $D E$ ，过点 $C$ 作 $C F / / D E$ 交 $A B$ 的延长线于点 $F$ ，连接 $F G$ ．

(1)、求证： $△ B D E$ ∽ $△ E F G$ ；

(2)、求 $∠ C F G$ 的度数；

(3)、若正方形 $A B C D$ 的边长为 $4$ ，点 $G$ 是 $D B$ 延长线上一点， $E G$ 交 $A B$ 的延长线于点 $E$ ，且 $D E$ 恰好经过 $B C$ 的中点，如图 $2$ ，其他条件不变，求 $\frac{F G}{D G}$ 的值．

查看试题解析
17. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 6$ 过点 $(2 ， 9)$ ，且交 $x$ 轴于 $A$ 、 $B$ 两点，交 $y$ 轴于点 $C$ ．其中 $B$ 点坐标 $(8 ， 0)$ ．

(1)、求抛物线的表达式；

(2)、点 $F$ 是直线 $B C$ 上方抛物线上的一动点，过点 $F$ 作 $F D ⊥ B C$ ，交 $B C$ 于点 $D$ ，过点 $F$ 作 $y$ 轴的平行线交直线 $B C$ 于点 $E$ ，过点 $D$ 作 $D G ⊥ E F$ ，交 $E F$ 于点 $G$ ，求 $D G$ 的最大值及此时点 $F$ 的坐标；

(3)、在（2）问中 $D G$ 取得最大值的条件下，将该抛物线沿射线 $C B$ 方向平移5个单位长度，点 $M$ 为平移后的抛物线的对称轴上一点，在平面内确定一点 $N$ ，使得以点 $A$ 、 $F$ 、 $M$ 、 $N$ 为顶点的四边形是以 $A F$ 为边长的菱形，写出所有符合条件的点 $N$ 的坐标，并写出求解点 $N$ 的坐标的一种情况的过程．

查看试题解析

人教版数学九年级下册27.2.2相似三角形的性质 同步分层训练培优题

一、选择题

二、填空题

三、解答题

四、综合题

人教版数学九年级下册27.2.2相似三角形的性质同步分层训练培优题