人教版数学九年级下册27.2.2相似三角形的性质 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 若两个相似三角形周长的比为 , 则这两个三角形对应边的比是( )A、 B、 C、 D、2. 若两个相似三角形的面积之比为 , 则它们对应角平分线之比为( )A、 B、 C、 D、3. 如果两个相似三角形的面积比是1:4,那么它们的周长比是( )A、1:16 B、1:4 C、1:6 D、1:24. 如图,在的正方形网格中,线段与交于点 , 若每个小正方形的边长为1,则的长为( )
 A、2 B、 C、 D、5. 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4 , 那么下列结论中,不正确的是 ( )
A、2 B、 C、 D、5. 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4 , 那么下列结论中,不正确的是 ( ) A、S1=S3 B、S2=2S1 C、S2=2S4 D、6. 如图,已知△ADE∽△ACB , 若AB=10,AC=8,AD=4,则AE的长是( )
A、S1=S3 B、S2=2S1 C、S2=2S4 D、6. 如图,已知△ADE∽△ACB , 若AB=10,AC=8,AD=4,则AE的长是( ) A、3.2 B、4 C、5 D、207. 如图是小阳设计利用光线来测量某古城墙高度的示意图,如果镜子P与古城墙的距离米,镜子P与小明的距离米,小明刚好从镜子中看到古城墙顶端点C , 小明眼睛距地面的高度米,解决本题应用什么光学知识,该古城墙的高度是( )
A、3.2 B、4 C、5 D、207. 如图是小阳设计利用光线来测量某古城墙高度的示意图,如果镜子P与古城墙的距离米,镜子P与小明的距离米,小明刚好从镜子中看到古城墙顶端点C , 小明眼睛距地面的高度米,解决本题应用什么光学知识,该古城墙的高度是( ) A、光的反射,米 B、光的折射,米 C、光沿直线传播,8米 D、光的反射,24米8. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A、光的反射,米 B、光的折射,米 C、光沿直线传播,8米 D、光的反射,24米8. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )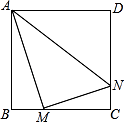 A、8 B、4 C、10 D、8
A、8 B、4 C、10 D、8二、填空题
-
9. 若两个相似三角形的相似比是1:2,则它们的周长比是 .10. 已知 , , , 的高为6,那么的高长为 .11. 如图,在 Rt△ABC中,∠ABC= 90°,D是边BC上一点,以BD为直径的半圆与边AC相切于点E.若AB=3,BC=4,则 BD=.
 12. 如图,将一个装有水的杯子倾斜放置在水平的桌面上,其截面可看作一个宽BC=6厘米,长CD=16厘米的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是厘米.
12. 如图,将一个装有水的杯子倾斜放置在水平的桌面上,其截面可看作一个宽BC=6厘米,长CD=16厘米的矩形.当水面触到杯口边缘时,边CD恰有一半露出水面,那么此时水面高度是厘米.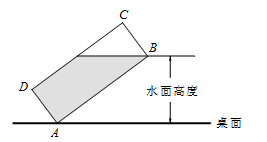 13. 如图,⊙O的半径为10,点P在⊙O上,点A在⊙O内,且AP=6,过点A作AP的垂线交QO于点B,C.若PC=15,则PB=.
13. 如图,⊙O的半径为10,点P在⊙O上,点A在⊙O内,且AP=6,过点A作AP的垂线交QO于点B,C.若PC=15,则PB=.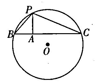
三、解答题
-
14. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,C为的中点,延长AD,BC相交于点P,连结AC.
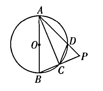 (1)、求证;AB=AP.(2)、当AB=10,DP=2时,求线段CP的长.15. 如图,在正方形中,点M、N分别在上, , , .
(1)、求证;AB=AP.(2)、当AB=10,DP=2时,求线段CP的长.15. 如图,在正方形中,点M、N分别在上, , , .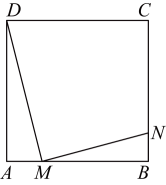 (1)、求证:;(2)、与有什么数量关系,请说明理由;(3)、与有什么位置关系,请说明理由.
(1)、求证:;(2)、与有什么数量关系,请说明理由;(3)、与有什么位置关系,请说明理由.四、综合题


