人教版数学九年级下册27.2.1相似三角形的判定 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 如图, , , 相交于点若 , , :( )
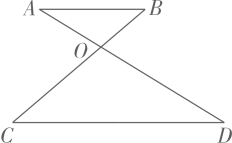 A、1:2 B、1:4 C、2:1 D、4:12. 如图,矩形中,点A在双曲线上,点B,C在x轴上,延长至点E,使 , 连接交y轴于点F,连接 , 则的面积为( )
A、1:2 B、1:4 C、2:1 D、4:12. 如图,矩形中,点A在双曲线上,点B,C在x轴上,延长至点E,使 , 连接交y轴于点F,连接 , 则的面积为( )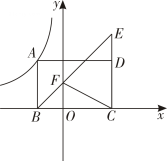 A、 B、 C、 D、3. 如图,在直角坐标系中,矩形的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为 , , 线段在边上移动,保持 , 当四边形的周长最小时,点E的坐标为 ( )
A、 B、 C、 D、3. 如图,在直角坐标系中,矩形的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为 , , 线段在边上移动,保持 , 当四边形的周长最小时,点E的坐标为 ( )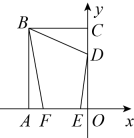 A、 B、 C、 D、4. 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为( )
A、 B、 C、 D、4. 如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为( ) A、4 B、3 C、2 D、15. 如图,AB是⊙O的直径,CD⊥AB于点E,连结CO并延长,交弦AD于点F.若AB=10,BE=2,则OF的长度是( )
A、4 B、3 C、2 D、15. 如图,AB是⊙O的直径,CD⊥AB于点E,连结CO并延长,交弦AD于点F.若AB=10,BE=2,则OF的长度是( )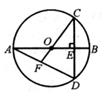 A、 B、3 C、 D、6. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A、 B、3 C、 D、6. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )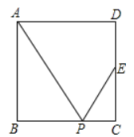 A、 B、 C、是的中点 D、7. 如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若 , 则的值为( )
A、 B、 C、是的中点 D、7. 如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若 , 则的值为( )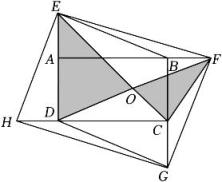 A、 B、 C、 D、8. 如图,在中, , 射线平分 , 于点D , 于点E , 若F为的中点,连接 . 下列结论:①;②;③;④ . 其中正确结论的序号是( )
A、 B、 C、 D、8. 如图,在中, , 射线平分 , 于点D , 于点E , 若F为的中点,连接 . 下列结论:①;②;③;④ . 其中正确结论的序号是( )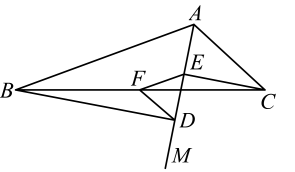 A、①②④ B、①③④ C、②③ D、①②③④
A、①②④ B、①③④ C、②③ D、①②③④二、填空题
-
9. 已知 , AD与BC相交于点O.若 , AD=10,则AO= .
 10. 如图,、相交于点O,点E、F分别在、上, , 如果 , , , , 那么 .
10. 如图,、相交于点O,点E、F分别在、上, , 如果 , , , , 那么 . 11. 直线l上的三个点A、B、C , 若满足BC=AB , 则称点C是点A关于点B的“半距点”.如图1,BC=AB , 此时点C就是点A关于点B的一个“半距点”.如图2若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm . 则MP=cm .
11. 直线l上的三个点A、B、C , 若满足BC=AB , 则称点C是点A关于点B的“半距点”.如图1,BC=AB , 此时点C就是点A关于点B的一个“半距点”.如图2若M、N、P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,MN=6cm . 则MP=cm . 12. 如图,正方形中,E为上一点,过B作于G,延长至点F使 , 延长交于点M,连接 , 若C为中点, , 则的长为 .
12. 如图,正方形中,E为上一点,过B作于G,延长至点F使 , 延长交于点M,连接 , 若C为中点, , 则的长为 . 13. 如图,矩形中,点 , 在轴上,交轴于点 , 点在上, , 连接交轴于点 , 过点作轴交于点 , 点在函数的图象上.若的面积为 , 则的值为 ;的面积与的面积差为 .
13. 如图,矩形中,点 , 在轴上,交轴于点 , 点在上, , 连接交轴于点 , 过点作轴交于点 , 点在函数的图象上.若的面积为 , 则的值为 ;的面积与的面积差为 .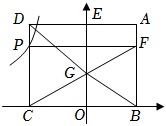
三、解答题
-
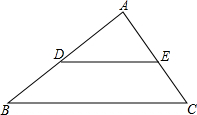
14. 如图,已知中, , 求BD的长.
 15. 如图,抛物线与x轴交于A、B两点,与y轴交于点C,直线过B、C两点,连接AC.
15. 如图,抛物线与x轴交于A、B两点,与y轴交于点C,直线过B、C两点,连接AC. (1)、求抛物线的解析式;(2)、求证:△AOC∽△ACB;(3)、抛物线对称轴上是否存在点P使得PC+PA的最小值?若存在,求出点P坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、求证:△AOC∽△ACB;(3)、抛物线对称轴上是否存在点P使得PC+PA的最小值?若存在,求出点P坐标;若不存在,请说明理由.四、作图题
-
16. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点.的顶点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,并保留适当的作图痕迹.
 (1)、在图①中的边上确定一点D , 连结 , 使得;(2)、在图②中的边上确定一点E , 连结 , 使得;(3)、在图③中的边上确定一点M , 边上确定一点N , 连结 , 使得 .
(1)、在图①中的边上确定一点D , 连结 , 使得;(2)、在图②中的边上确定一点E , 连结 , 使得;(3)、在图③中的边上确定一点M , 边上确定一点N , 连结 , 使得 .五、综合题

