人教版数学九年级下册27.2.1相似三角形的判定 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 如图, , 那么下列结论正确的是( )
 A、 B、 C、 D、2. 已知 , , , 成比例线段,其中 , , , 则( )A、8cm B、9.5cm C、4cm D、4.5cm3. 如图,在中,点分别是边上的点, , 且 , 则等于( )
A、 B、 C、 D、2. 已知 , , , 成比例线段,其中 , , , 则( )A、8cm B、9.5cm C、4cm D、4.5cm3. 如图,在中,点分别是边上的点, , 且 , 则等于( ) A、5:8 B、3:8 C、3:5 D、2:54. 已知在中,点、分别在边、上,那么下列条件中不能够判断的是( )A、 B、 C、 D、5. 如图,在中,点分别在边上, . 若 , 下列结论正确的是( )
A、5:8 B、3:8 C、3:5 D、2:54. 已知在中,点、分别在边、上,那么下列条件中不能够判断的是( )A、 B、 C、 D、5. 如图,在中,点分别在边上, . 若 , 下列结论正确的是( )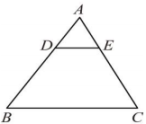 A、 B、 C、 D、6. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、
A、 B、 C、 D、6. 如图,在中, . 将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A、 B、
B、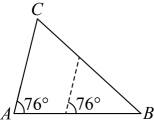 C、
C、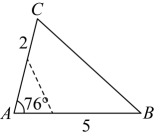 D、
D、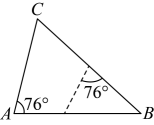 7. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( )
7. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( ) A、 B、 C、 D、8. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( )
A、 B、 C、 D、8. 如图正方形 , 点分别在边上,且 , 把绕点沿逆时针方向旋转得到 , 连接交于点 , 连接 , 并在上截取 , 连接 , 有如下结论:①;②始终平分;③;④;⑤垂直平分 , 上述结论中,所有正确的个数是( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
9. 如图,在 中,D、E分别是边 、 上的点,且 .若 , , ,则 的长为 .
 10. 如图,在矩形中,是边的中点,连接交对角线于点 , 则的长为 .
10. 如图,在矩形中,是边的中点,连接交对角线于点 , 则的长为 . 11. 如图,已知在△中,是边上的一点,连结.当满足条件时,△∽△(写一个即可).
11. 如图,已知在△中,是边上的一点,连结.当满足条件时,△∽△(写一个即可).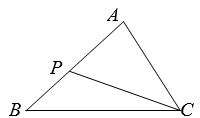 12. 如图,在正方形网格上,若使 , 则点P应在 .
12. 如图,在正方形网格上,若使 , 则点P应在 .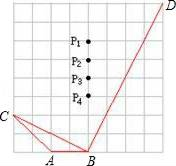 13. 如图,直线与x轴、y轴分别交于点A、B , 一动点P从点A出发,沿的路线运动到点B停止,C是的中点,沿直线PC截 , 若得到的三角形与相似,则点P的坐标是 .
13. 如图,直线与x轴、y轴分别交于点A、B , 一动点P从点A出发,沿的路线运动到点B停止,C是的中点,沿直线PC截 , 若得到的三角形与相似,则点P的坐标是 .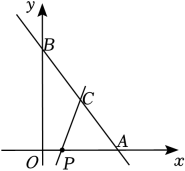
三、解答题
-
14. 如图,在中,经 , CD是边AB上的高.
 (1)、求证:;(2)、若 , , 求BD的长.15. 如图所示,点A,B,C,D在☉O上,=.求证:
(1)、求证:;(2)、若 , , 求BD的长.15. 如图所示,点A,B,C,D在☉O上,=.求证: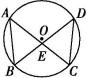 (1)、BD=AC;(2)、△ABE∽△DCE.
(1)、BD=AC;(2)、△ABE∽△DCE.四、综合题
-
16. 如图,在△ABC中,D , E分别是AB和AC上的点,且DE∥BC .
 (1)、若AD=5,DB=6,EC=12,求AE的长;(2)、若AB=10,AD=4,AE=6,求EC的长.17. 已知:如图,在中, , 点由点出发沿方向向点匀速运动,速度为;点由点出发沿方向向点匀速运动,速度为:若设运动的时间为 , 解答下列问题:
(1)、若AD=5,DB=6,EC=12,求AE的长;(2)、若AB=10,AD=4,AE=6,求EC的长.17. 已知:如图,在中, , 点由点出发沿方向向点匀速运动,速度为;点由点出发沿方向向点匀速运动,速度为:若设运动的时间为 , 解答下列问题:


图① 图② 图③
(1)、如图①,连接 , 当为何值时 , 并说明理由;(2)、如图②,当点运动时,是否存在某一时刻 , 使得点在线段的垂直平分线上,请说明理由;(3)、如图③,当点运动时,线段上是否存在一点 , 使得四边形为荾形?若存在,试求出长:若不存在,请说明理由.