人教版数学九年级下册27.1 图形的相似 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 手工制作课上,小丽利用一些花布的边角料,剪裁后装饰手工画,如图,下面四个图案是她剪裁出的空心的直角三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD相似的是( )A、
2. 已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD相似的是( )A、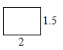 B、
B、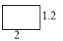 C、
C、 D、
D、 3. 下列判断正确的是( )A、任意两个等腰直角三角形相似 B、任意两个直角三角形相似 C、任意两个等腰三角形相似 D、菱形都相似4. 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,连接CD,若∠ACD=2∠B, , 则的值是( )
3. 下列判断正确的是( )A、任意两个等腰直角三角形相似 B、任意两个直角三角形相似 C、任意两个等腰三角形相似 D、菱形都相似4. 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,连接CD,若∠ACD=2∠B, , 则的值是( ) A、 B、 C、 D、5. 要拼出和图①中的菱形相似的较长对角线为88cm的大菱形(如图②) ,需要如图①的菱形的个数是( ).
A、 B、 C、 D、5. 要拼出和图①中的菱形相似的较长对角线为88cm的大菱形(如图②) ,需要如图①的菱形的个数是( ). A、11个 B、121个 C、22个 D、242 个6. 如图所示,内外两个矩形相似,且对应边平行,则下列结论中,正确的是( ).
A、11个 B、121个 C、22个 D、242 个6. 如图所示,内外两个矩形相似,且对应边平行,则下列结论中,正确的是( ).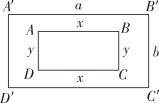 A、 B、 C、 D、以上答案都不对7. 如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推,若每次对开得到的矩形都相似,则等于( ).
A、 B、 C、 D、以上答案都不对7. 如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推,若每次对开得到的矩形都相似,则等于( ). A、0.618 B、 C、 D、28. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、0.618 B、 C、 D、28. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )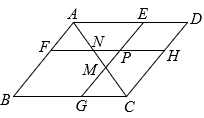 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 两个相似多边形的周长比是2:3,其中较小多边形的面积为12 ,则较大多边形的面积为 .10. 已知四边形ABCD与四边形A'B'C′D'相似,边AB与边A'B'是对应边,S四边形ABCD:S四边形A'B′C′D'=2:4,AB=2,则A'B'=.11. 复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为.
 12. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
12. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .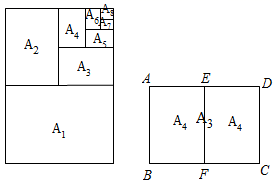 13. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是.
13. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是.
三、解答题
-
14. 如图,四边形ABCD的四边形EFGH .若AB=18,EF=4,FG=6,∠B=77°,∠C=83°,∠E=117°,求线段BC的长和∠H的大小.
 15. 用木条制成如图的形式,A、B、C三点钉上钉子,在D和D′处加上粉笔,当用D′画图时,在D处的笔同时也画出一个图形.请问:这样画出的两个图形是相似图形吗?
15. 用木条制成如图的形式,A、B、C三点钉上钉子,在D和D′处加上粉笔,当用D′画图时,在D处的笔同时也画出一个图形.请问:这样画出的两个图形是相似图形吗?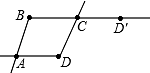
四、作图题
-
16. 如图,△ABC的三个顶点坐标分别为A(2,3),B(3,1),C(5,4).
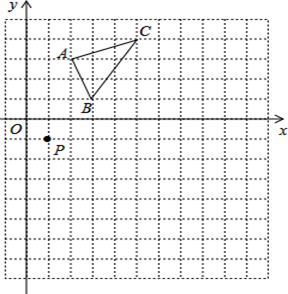
⑴画出△ABC关于x轴对称的△A1B1C1;
⑵以点P(1,﹣1)为位似中心,在如图所示的网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1;
⑶画出△ABC绕点C逆时针旋转90°的△A′B′C′,并写出线段BC扫过的面积
五、综合题
-
17. 如图,在直角坐标中,矩形的顶点O与坐标原点重合,顶点A、C分别在x轴和y轴上,点B的坐标为 , 反比例函数是的图象经过的中点D,且与交于点E,连接 .
 (1)、求k的值及点E的坐标;(2)、若点F是边上一点,且 , 求直线的解析式.(3)、若点P在y轴上,且的面积与四边形的面积相等,求点P的坐标.18. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?
(1)、求k的值及点E的坐标;(2)、若点F是边上一点,且 , 求直线的解析式.(3)、若点P在y轴上,且的面积与四边形的面积相等,求点P的坐标.18. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
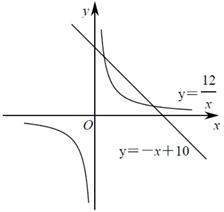
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
-