2023-2024学年人教版初中数学九年级下册26.2 实际问题与反比例函数 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 购买 斤水果需 元,购买一斤水果的单价 与 的关系式是( )A、 B、 ( 为自然数) C、 ( 为整数) D、 ( 为正整数)2. 小明学习了物理中的杠杆平衡原理发现:阻力 阻力臂 动力 动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力 (单位:N)关于动力臂 (单位:m)的函数图象大致是( )A、
 B、
B、 C、
C、 D、
D、 3. 某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).
3. 某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).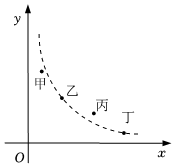 A、甲 B、乙 C、丙 D、丁4.
A、甲 B、乙 C、丙 D、丁4.如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )
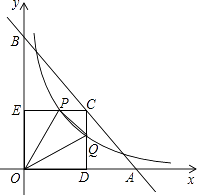 A、4 B、2 C、 D、5. 已知正比例函数y=2x与反比例函数y=的图象相交于A,B两点,若A点的坐标为(1,2),则B点的坐标为( )A、(1,﹣2) B、(﹣1,2) C、(﹣1,﹣2) D、(2,1)6. 如果反比例函数y=的图象经过点(1,﹣2),那么k的值是( )A、- B、 C、-2 D、27. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板人的质量m之间的函数关系式为 , 其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( )
A、4 B、2 C、 D、5. 已知正比例函数y=2x与反比例函数y=的图象相交于A,B两点,若A点的坐标为(1,2),则B点的坐标为( )A、(1,﹣2) B、(﹣1,2) C、(﹣1,﹣2) D、(2,1)6. 如果反比例函数y=的图象经过点(1,﹣2),那么k的值是( )A、- B、 C、-2 D、27. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板人的质量m之间的函数关系式为 , 其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( ) A、用含I的代数式表示为 B、电子体重秤可称的最大质量为120千克 C、当时,若电源电压U为12(伏),则定值电阻最小为70(欧) D、当时,若定值电阻为40(欧),则电源电压U最大为10(伏)8. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A、用含I的代数式表示为 B、电子体重秤可称的最大质量为120千克 C、当时,若电源电压U为12(伏),则定值电阻最小为70(欧) D、当时,若定值电阻为40(欧),则电源电压U最大为10(伏)8. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )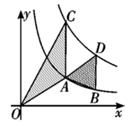 A、4 B、3 C、2 D、
A、4 B、3 C、2 D、二、填空题
-
9. 由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值始终保持 , 发现通过滑动变阻器的电流与滑动变阻器的电阻成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过 , 则滑动变阻器阻值的范围是 .
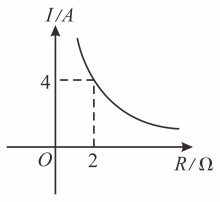 10. 某型号汽车行驶时功率一定,行驶速度(单位:m/s)与所受阻力(单位:N)是反比例函数关系,其图象如图所示.若该型号汽车在某段公路上行驶时速度为 , 则所受阻力为 .
10. 某型号汽车行驶时功率一定,行驶速度(单位:m/s)与所受阻力(单位:N)是反比例函数关系,其图象如图所示.若该型号汽车在某段公路上行驶时速度为 , 则所受阻力为 . 11. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .12. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
11. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,且当时, . 当气球内的气体压强大于时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 .12. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
①若 , 则.
②若 , 则的值为.
13. 如图,在平面直角坐标系中,四边形ABCD是矩形,已知点A(0,2),AB=2AD,点C,D在反比例函数y= (k>0)的图象上,AB与x轴的正半轴相交于点E,若点E为AB的中点,则k的值为
三、解答题
-
14. 如图,直线与双曲线相交于点 , 轴于点 , 以为边在右侧作正方形 , 与双曲线相交于点 , 连结、 .
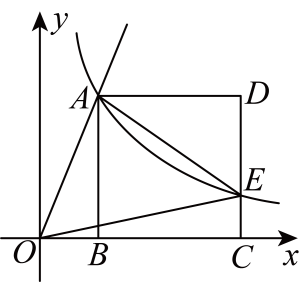 (1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.15.
(1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.15.如图,已知一次函数y= x﹣3与反比例函数 的图象相交于点A(4,n),与 轴相交于点B.
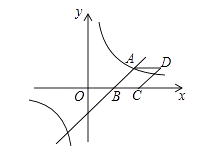 (1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;(3)、考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.
(1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;(3)、考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.
四、综合题
-
16. 某品牌饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y℃与开机时间x分满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中水温y℃与开机时间x分成反比例关系),当水温降至20℃时,饮水机又自动开始加热,…,重复上述程序(如图所示),
 (1)、分别求出和时的函数关系式,并求出t的值;(2)、两次加热之间,水温保持不低于40℃有多长时间?(3)、开机后50分钟时,求水的温度是多少℃?17. 在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上,函数的图象与BC边相交于点M(点M不与点B重合),与AB边相交于点N.
(1)、分别求出和时的函数关系式,并求出t的值;(2)、两次加热之间,水温保持不低于40℃有多长时间?(3)、开机后50分钟时,求水的温度是多少℃?17. 在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴上,函数的图象与BC边相交于点M(点M不与点B重合),与AB边相交于点N. (1)、如图①,若点B的坐标为(4,2),M为CB中点,求k的值和点N的坐标.(2)、如图②,连结OB,过点M作MQ⊥OB,垂足为Q.若k=1,MB=2CM时,设OB长为m,MQ长为n,求m与n的函数关系式.
(1)、如图①,若点B的坐标为(4,2),M为CB中点,求k的值和点N的坐标.(2)、如图②,连结OB,过点M作MQ⊥OB,垂足为Q.若k=1,MB=2CM时,设OB长为m,MQ长为n,求m与n的函数关系式.