2023-2024学年人教版初中数学九年级下册26.2 实际问题与反比例函数 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
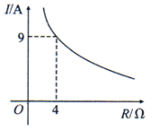
1. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
 A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,2. 某电子商城推出分期付款购买电脑的活动,一台电脑的售价为1.2万元,前期付款4000元,后期每个月分期付一定的数额,则每个月的付款额 (元)与付款月数 之间的函数关系式是( )A、(x为正整数) B、 C、 D、3. 下列各问题中,两个变量之间的关系不是反比例函数的是A、小明完成100m赛跑时,时间t(s)与跑步的平均速度v(m/s)之间的关系. B、菱形的面积为48cm2 , 它的两条对角线的长为y(cm)与x(cm)的关系. C、一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时,压强p与受力面积S之间的关系.4. 安乡子龙汽车站与常德市柳叶湖汽车站相距约 , 则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间小时与行驶速度千米时之间的函数图象大致是( )A、
A、函数解析式为 B、蓄电池的电压是18V C、当时, D、当时,2. 某电子商城推出分期付款购买电脑的活动,一台电脑的售价为1.2万元,前期付款4000元,后期每个月分期付一定的数额,则每个月的付款额 (元)与付款月数 之间的函数关系式是( )A、(x为正整数) B、 C、 D、3. 下列各问题中,两个变量之间的关系不是反比例函数的是A、小明完成100m赛跑时,时间t(s)与跑步的平均速度v(m/s)之间的关系. B、菱形的面积为48cm2 , 它的两条对角线的长为y(cm)与x(cm)的关系. C、一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时,压强p与受力面积S之间的关系.4. 安乡子龙汽车站与常德市柳叶湖汽车站相距约 , 则汽车由子龙汽车站行驶到柳叶湖汽车站所用时间小时与行驶速度千米时之间的函数图象大致是( )A、 B、
B、 C、
C、 D、
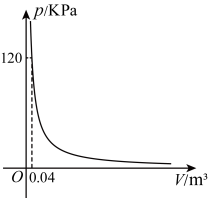
D、 5. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
5. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )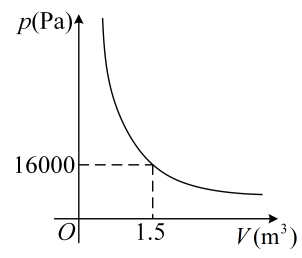 A、不小于 B、不大于 C、不小于 D、不大于6. 下面的三个问题中都有两个变量:
A、不小于 B、不大于 C、不小于 D、不大于6. 下面的三个问题中都有两个变量:
京沪铁路全程为 , 某次列车的平均速度单位:与此次列车的全程运行时间单位:;
已知北京市的总面积为 , 人均占有面积单位:人与全市总人口单位:人;
某油箱容量是的汽车,加满汽油后开了时,油箱中汽油大约消耗了油箱中的剩油量与加满汽油后汽车行驶的路程 .
其中,变量与变量之间的函数关系可以用如图所示的图象表示的是( ) A、 B、 C、 D、7. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点 , 交AC于点 , 反比例函数的图象经过线段DC的中点 , 若 , 则AG的长为( )
A、 B、 C、 D、7. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点 , 交AC于点 , 反比例函数的图象经过线段DC的中点 , 若 , 则AG的长为( ) A、 B、 C、 D、8. 如图,直线分别交x轴、y轴于点C,D,点P为反比例函数在第一象限内图像上的一点,过点P分别作x轴、y轴的垂线交直线于点A,B,且 , 则下列结论错误的是( )
A、 B、 C、 D、8. 如图,直线分别交x轴、y轴于点C,D,点P为反比例函数在第一象限内图像上的一点,过点P分别作x轴、y轴的垂线交直线于点A,B,且 , 则下列结论错误的是( ) A、与相似 B、 C、 D、
A、与相似 B、 C、 D、二、填空题
-
9. 电流通过导线时会产生热量Q(单位:J)与通过导体的电流I(单位:A)有如下关系: , 其中R表示通电电阻(单位:)、t表示通电时间(单位:s).已知一台带有USB借口的小电风扇线圈电阻为 , 正常工作1分钟后线圈产生的热量为15J,则通过导体的电流为A.10. 验光师通过检测发现近视眼镜的度数度与镜片焦距米成反比例,关于的函数图象如图所示经过一段时间的矫正治疗后,小雪的镜片焦距由米调整到米,则近视眼镜的度数减少了度
 11. 我们知道,描点法是画函数图象的重要方法,通过描点画图可知,函数y=的图象可由函数y=的图象向平移一个单位得到.12. 为预防流感,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)之间的函数关系如图所示.已知在药物燃烧阶段,y与x成正比例,燃烧完后y与x成反比例.现测得药物10min燃烧完,此时教室内每立方米空气含药量8mg , 当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经过min后教室内的空气才能达到安全要求.
11. 我们知道,描点法是画函数图象的重要方法,通过描点画图可知,函数y=的图象可由函数y=的图象向平移一个单位得到.12. 为预防流感,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)之间的函数关系如图所示.已知在药物燃烧阶段,y与x成正比例,燃烧完后y与x成反比例.现测得药物10min燃烧完,此时教室内每立方米空气含药量8mg , 当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经过min后教室内的空气才能达到安全要求. 13. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接 . 若 , 则的值是 .
13. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接 . 若 , 则的值是 .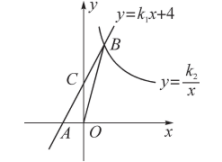
三、解答题
-
14. 已知反比例函数的图象经过点.(1)、求k的值;(2)、点 , 均在反比例函数的图象上,若 , 直接写出 , 的大小关系.15. 某人采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg , 请你根据题中所提供的信息,解答下列问题.
 (1)、药物燃烧时y关于x的函数关系式为 , 自变量x的取值范围是;药物燃烧后y与x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6mg时学生可以进教室,那么从消毒开始,至少多少分钟后学生才能回到教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,此次消毒是否有效?为什么?
(1)、药物燃烧时y关于x的函数关系式为 , 自变量x的取值范围是;药物燃烧后y与x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6mg时学生可以进教室,那么从消毒开始,至少多少分钟后学生才能回到教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,此次消毒是否有效?为什么?四、综合题