2023-2024学年人教版初中数学九年级下册26.2 实际问题与反比例函数同步分层训练基础题

试卷更新日期：2024-01-20 类型：同步测试

进入出卷网下载

一、选择题

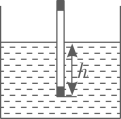
1. 若反比例函数的图象过点（3，2），那么下列各点中在此函数图象上的点是（）

A、（-2，3） B、（-3，2） C、（-3，-2） D、（4，1）

查看试题解析
2. 对于反比例函数 $y = - \frac{2}{x}$ ，下列说法不正确的是（）

A、点 $(- 2 ， 1)$ 在它的图象上 B、它的图象在第二、四象限 C、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 D、当 $x < 0$ 时， $y$ 随 $x$ 的增大而减小

查看试题解析
3. 正在建设中的临滕高速是我省“十四五”重点建设项目．一段工程施工需要运送土石方总量为 $1 0^{5} m^{3}$ ，设土石方日平均运送量为V（单位： $m^{3}$ /天），完成运送任务所需要的时间为t（单位：天），则V与t满足（）

A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系

查看试题解析
4. 某闭合并联电路中，各支路电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例，如图表示该电路I与电阻R的函数关系图象，若该电路中某导体电阻为 $4 Ω$ ，则导体内通过的电流为(　　)

A、 $2 A$ B、 $2.5 A$ C、 $5 A$ D、 $10 A$

查看试题解析
5. 如果100N的压力F作用于物体上，产生的压强p要大于1000Pa，则下列关于物体受力面积S(m²)的说法正确的是（）

A、S小于0.1m² B、S大于0.1m² C、S小于10m² D、S大于10m²

查看试题解析
6. 近视眼镜的度数 $y$ （度）与镜片焦距 $x$ （m）成反比例，已知200度近视眼镜的镜片焦距为0.5m，若某近视眼镜片的焦距为0.25m，则该眼镜片的度数为（）

A、100度 B、300度 C、400度 D、600度

查看试题解析
7. 如图， $A$ ， $B$ 是反比例函数 $y = \frac{4}{x}$ 在第一象限内的图象上的两点，且 $A$ ， $B$ 两点的横坐标分别是2和4，则 $△ O A B$ 的面积是（）

A、3 B、2 C、 $3.5$ D、4

查看试题解析
8. 某厂现有300吨煤，这些煤能烧的天数 $y$ 与平均每天烧的吨数 $x$ 之间的函数关系是（）

A、 $y = \frac{300}{x} (x > 0)$ B、 $y = \frac{300}{x} (x \geq 0)$ C、 $y = 300 x (x \geq 0)$ D、 $y = 300 x (x > 0)$

查看试题解析

二、填空题

9. 一个游泳池的容积为 $2000 m^{3}$ ，游泳池注满水所用时间 $t$ 与注水速度 $v$ （填“成正比例”、“成反比例”、“不成比例”）．

查看试题解析
10. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例（即 $y = \frac{k}{x} (k \neq 0)$ ），已知200度近视眼镜的镜片焦距为0.5m ，则y与x之间的函数关系式是．

查看试题解析
11. 科技小组为了验证某电路的电压U（V）、电流I（A）、电阻 $R (Ω)$ 三者之间的关系： $I = \frac{U}{R}$ ，测得数据如下：

$R (Ω)$

100

200

220

400

$I (A)$

2.2

1.1

1

0.55

那么，当电阻 $R = 55 Ω$ 时，电流 $I =$ A.

查看试题解析
12. 已知蓄电池的电压恒定，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，流过的电流是2A，那么此用电器的电阻是Ω.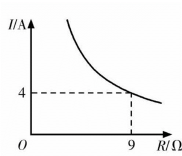

查看试题解析
13. 列车从甲地驶往乙地．行完全程所需的时间 $t (h)$ 与行驶的平均速度 $v (k m / h)$ 之间的反比例函数关系如图所示．若列车要在 $2.5 h$ 内到达，则速度至少需要提高到 $k m / h$ ．

查看试题解析

三、解答题

14. 国庆期间，小李自驾小汽车从家到银屏山旅游．查询导航得知，当他的小汽车保持80km/h的速度行驶3h可以到达银屏山．若该小汽车匀速行驶的速度为vkm/h，行驶的时间为th．

(1)、求v关于t的函数表达式；

(2)、若返回时，该小汽车匀速行驶的速度为60km/h，假设他返回与去时的路况和其他因素一致，求他从银屏山回到家需要几小时．

查看试题解析
15. 已知平面直角坐标系中，直线AB与反比例函数y= $\frac{k}{x}$ （x＞0）的图象交于点A（1，3）和点B（3，n），与x轴交于点C ，与y轴交于点D ．

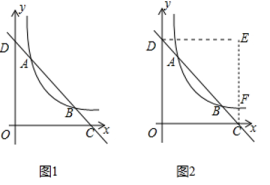(1)、求反比例函数的表达式及n的值；

(2)、将△OCD沿直线AB翻折，点O落在第一象限内的点E处，EC与反比例函数的图象交于点F ．
①请求出点F的坐标；
②将线段BF绕点B旋转，在旋转过程中，求线段OF的最大值．

查看试题解析

四、综合题

16. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m）的反比例函数，其图象如图所示．

(1)、求这个函数的表达式；

(2)、当气球的体积是1m³时，气球内的气压是多少千帕？

查看试题解析
17. 科学课上，同学用自制密度计测量液体的密度．密度计悬浮在不同的液体中时，浸在液体中的高度h（单位：cm）是液体的密度 $ρ$ （单位： $g / c m^{3}$ ）的反比例函数，当密度计悬浮在密度为 $1 g / c m^{3}$ 的水中时， $h = 20 c m$ ．

(1)、求h关于 $ρ$ 的函数解析式．

(2)、当密度计悬浮在另一种液体中时， $h = 25 c m$ ，求该液体的密度 $ρ$ ．

查看试题解析

$R (Ω)$	100	200	220	400
$I (A)$	2.2	1.1	1	0.55

2023-2024学年人教版初中数学九年级下册26.2 实际问题与反比例函数 同步分层训练基础题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学九年级下册26.2 实际问题与反比例函数同步分层训练基础题