2023-2024学年人教版初中数学九年级下册26.1.2 反比例函数的图像和性质 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、2. 下列给出的各个点中,在双曲线上的点为( )A、 B、 C、 D、3. 正比例函数y=2x与反比例函数y= 的图象或性质的共有特征之一是( )A、函数值y随x的增大而增大 B、图象在第一、三象限都有分布 C、图象与坐标轴有交点 D、图象经过点(2,1)4. 已知点在下列某一函数图象上,且那么这个函数是( )A、 B、 C、 D、5. 抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y= 在同一平面直角坐标系内的图象大致为( )
 A、
A、 B、
B、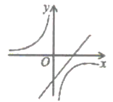 C、
C、 D、
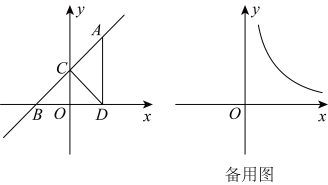
D、 6. 已知反比例函数 ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(-4,-3)在函数图象上 C、y随x的增大而增大 D、若点(-2,y1)和(-1,y2)在该函数图象上,则y1<y27. 在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B , C的横坐标都是3, , 点D在上,且其横坐标为1,若反比例函数()的图像经过点B , D , 则k的值是( )
6. 已知反比例函数 ,下列说法中正确的是( )A、该函数的图象分布在第一、三象限 B、点(-4,-3)在函数图象上 C、y随x的增大而增大 D、若点(-2,y1)和(-1,y2)在该函数图象上,则y1<y27. 在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B , C的横坐标都是3, , 点D在上,且其横坐标为1,若反比例函数()的图像经过点B , D , 则k的值是( ) A、1 B、2 C、3 D、8. 函数图象与有交点 , 且满足 , 则的取值范围是( )A、 B、或2 C、 D、或
A、1 B、2 C、3 D、8. 函数图象与有交点 , 且满足 , 则的取值范围是( )A、 B、或2 C、 D、或二、填空题
-
9. 若点 , 都在反比例函数的图象上,则(填“>”或“<”).10. 反比例函数的图象分布在第一、三象限内,则的取值范围为 .11. 在平面直角坐标系中,若函数的图象经过点和 , 则m的值为 .12. 如果反比例函数y=的图象位于第二、四象限内,那么k的取值范围为 .13. 在直角坐标平面内,函数的图像在同一个象限内经过A、B两点,且 . 过点作轴垂线,垂足为点 , 连接、、 , 若 , 则点的坐标是 .
三、解答题
-
14. 已知反比例函数的图象经过第一、三象限.(1)、求的取值范围;(2)、若 , 此函数的图象过第一象限的两点 , , 且 , 求的取值范围.15. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(为的整数),函数的图象为曲线 .
 (1)、则的坐标是 .(2)、若曲线过时,求出的值,并说明此时曲线是否过 .(3)、若曲线使得这些点分布在它的两侧,每侧各2个点,的取值范围是 .
(1)、则的坐标是 .(2)、若曲线过时,求出的值,并说明此时曲线是否过 .(3)、若曲线使得这些点分布在它的两侧,每侧各2个点,的取值范围是 .四、综合题