2023-2024学年人教版初中数学八年级下册17.2 勾股定理的逆定理同步分层训练培优题

试卷更新日期：2024-01-20 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，直角 $△ A B C$ 中， $A C = 7$ ， $A B = 25$ ，则内部五个小直角三角形的周长为（）．

A、32 B、56 C、31 D、55

查看试题解析
2. 如图是一张探宝图，根据图中的尺寸，起点 $A$ 到终点 $B$ 的距离是（）

A、 $10$ B、 $8$ C、 $\sqrt{113}$ D、 $9$

查看试题解析
3. 下列各组数中，不能判定△ABC为直角三角形是（）

A、 $a = 1 ， b = \sqrt{2} ， c = \sqrt{3}$ B、∠A＋∠B＝∠C C、a＝5，b＝9，c＝13 D、 $a^{2} + b^{2} = c^{2}$

查看试题解析
4. 如图，以 $R t △ A B C$ 为直径分别向外作半圆，若 $S_{1} = 10$ ， $S_{3} = 8$ ，则 $S_{2} =$ （）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
5. $△ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ．下列条件： $① ∠ A = ∠ B - ∠ C$ ； $② a^{2} = (b + c) (b - c)$ ； $③ ∠ A$ ∶ $∠ B$ ∶ $∠ C = 3$ ∶ $4$ ∶ $5$ ； $④ a$ ∶ $b$ ∶ $c = 5$ ∶ $12$ ∶ $13$ ．其中能判断 $△ A B C$ 是直角三角形的个数有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
6. 如图1，在 $R t △ A B C$ 中，点P从点C出发，设点P的运动距离为x， $A P$ 的长为y，则当点P为 $B C$ 中点时， $A P$ 的长为（）

A、5 B、 $5 \sqrt{2}$ C、 $2 \sqrt{13}$ D、8

查看试题解析
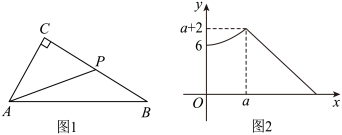7. 如图，在平面直角坐标系中，点 $A (- 2 ， 2)$ ， $B (2 ， 1)$ ，点 $P (x ， 0)$ 是 $x$ 轴上的一个动点．结合图形得出式子 $\sqrt{(x + 2)^{2} + 4} + \sqrt{(2 - x)^{2} + 1}$ 的最小值是（）

A、3 B、 $\sqrt{17}$ C、5 D、 $2 \sqrt{2} + \sqrt{5}$

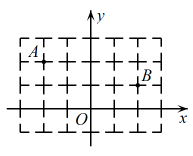查看试题解析
8. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数．某同学将自探究勾股数的过程列成下表，观察表中每列数的规律，可知 $x + y$ 的值为（）
a
b
c
3
4
5
8
6
10
15
8
17
24
10
26
…
…
…
x
14
y

A、67 B、34 C、98 D、73

查看试题解析

二、填空题

9. 某楼梯如图所示，欲在楼梯上铺设红色地毯，已知这种地毯每平方米售价为30元，楼梯宽为2m，则购买这种地毯至少需要元．

查看试题解析
10. 如图，一只蚂蚁沿着边长为2的正方体表面从点4出发，经过3个面爬到点B，如果它运动的路径是最短的，则最短路径的是长为.

查看试题解析
11. 如图是一个三级台阶，每一级的长，宽和高分别是50cm，30cm，10cm，A和B是这个台阶的两个相对的端点，若一只壁虎从A点出发沿着台阶面爬到B点，则壁虎爬行的最短路线的长是．

查看试题解析
12. 如图，已知Rt△ABC，∠C=90°，AC=BC=2，点M，N分别为CB，CA上的动点，且始终保持BM=CN，则AM+BN的最小值为．

查看试题解析
13. 如图，某开发区有一块四边形的空地ABCD，现计划在空地上种植草皮，经测量∠A＝90°，AB＝3m，BC＝12m，CD＝13m，DA＝4m，若每平方米草皮需要200元，则要投入元.

查看试题解析

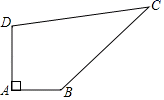
三、解答题

14. 如图，小旭放风筝时，风筝线断了，风筝挂在了树上．他想知道风筝距地面的高度．于是他先拉住风筝线垂直到地面上，发现风筝线多出1米，然后把风筝线沿直线向后拉开5米，发现风筝线末端刚好接触地面（如图为示意图）．请你帮小旭求出风筝距离地面的高度 $A B$ ．

查看试题解析
15. 阅读：能够成为直角三角形的三边长的三个正整数a，b，c，称为勾股数．世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》，其勾股数组的公式为 ${\begin{matrix} \begin{array}{l} a = \frac{1}{2} (m^{2} - n^{2}) \\ b = m n \end{array} \\ c = \frac{1}{2} (m^{2} + n^{2}) \end{matrix}$ 其中m＞n＞0，m，n是互质的奇数．
应用：当n＝1时，求有一边长为5的直角三角形的另外两条边的长．

查看试题解析

四、综合题

16. 如图1，在正方形 $A B C D$ 中，E是 $A B$ 的中点．

(1)、若 $A D = 4$ ，求 $D E$ 的长．

(2)、如图2，F是线段 $B C$ 上的一点，且 $A E = 2 B F$ ，求证： $△ D E F$ 是直角三角形．

(3)、如图3是一个正方体，棱长 $A D = 4$ ， $A B$ 的中点E处有一只蚂蚁，蚂蚁从 $E$ 处出发在正方体表面爬行，经过 $C D$ 上某点P处后继续沿直线方向爬到正方体的顶点G处．当 $E P + P G$ 的值最小时，求 $D P$ 的长．

查看试题解析
17. 如图，一条笔直的竹竿斜靠在一道垂直于地面的墙面上，一端在墙面A处，另一端在地面B处，墙角记为点C.

(1)、若 $A B = 6.5$ 米， $B C = 2.5$ 米.
①竹竿的顶端A沿墙下滑1米，那么点B将向外移动多少米？

②竹竿的顶端从A处沿墙 $A C$ 下滑的距离与点B向外移动的距离，有可能相等吗？如果不可能，请说明理由；如果可能，请求出移动的距离（保留根号）.

(2)、若 $A C = B C$ ，则顶端A下滑的距离与底端B外移的距离，有可能相等吗？若能相等，请说明理由；若不等，请比较顶端A下滑的距离与底端B外移的距离的大小.

查看试题解析

a	b	c
3	4	5
8	6	10
15	8	17
24	10	26
…	…	…
x	14	y

2023-2024学年人教版初中数学八年级下册17.2 勾股定理的逆定理 同步分层训练培优题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学八年级下册17.2 勾股定理的逆定理同步分层训练培优题