人教版初中数学八年级下册17.2 勾股定理的逆定理 同步分层训练提升题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 下列图各组数中,是勾股数的是( )A、6,8,12 B、0.6,0.8,1 C、8,15,16 D、9,12,152. 如图,在的网格中,每个小正方形的边长均为1,点A、B都在格点上,则下列结论错误的是( )
 A、的面积为10 B、 C、 D、点A到直线的距离是23. 三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形4. 如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )
A、的面积为10 B、 C、 D、点A到直线的距离是23. 三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形4. 如图,是台阶的示意图.已知每个台阶的宽度都是20cm,每个台阶的高度都是10cm,连接AB,则AB等于( )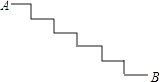 A、120cm B、130cm C、140cm D、150cm5. 下列各组数是三角形的三边,不能组成直角三角形的一组数是( )A、3,4,5 B、6,8,10 C、1.5,2,2.5 D、 , ,6. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
A、120cm B、130cm C、140cm D、150cm5. 下列各组数是三角形的三边,不能组成直角三角形的一组数是( )A、3,4,5 B、6,8,10 C、1.5,2,2.5 D、 , ,6. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )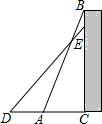 A、0.4 B、0.6 C、0.7 D、0.87. 矩形 中, 是 中点,如果 , , 那么 的长为 ( )
A、0.4 B、0.6 C、0.7 D、0.87. 矩形 中, 是 中点,如果 , , 那么 的长为 ( ) A、 B、 C、 D、38. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( )
A、 B、 C、 D、38. 如图,为等腰直角三角形, , 以斜边为直角边作等腰直角三角形 , 再以为直角边作等腰直角三角形 , , 按此规律作下去,则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要元.
 10. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 , 正方形A的面积是的面积是的面积是 , 则的面积为 .
10. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 , 正方形A的面积是的面积是的面积是 , 则的面积为 . 11. 在中, , , 分别是 , , 所对的边.若 , , , 则最长边上的高是 .12. 如图,“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形,是我国古代数学的骄傲,巧妙地利用面积关系证明了勾股定理.已知小正方形的面积是1,直角三角形的两直角边分别为a、b且 , 则图中大正方形的边长为 .
11. 在中, , , 分别是 , , 所对的边.若 , , , 则最长边上的高是 .12. 如图,“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形,是我国古代数学的骄傲,巧妙地利用面积关系证明了勾股定理.已知小正方形的面积是1,直角三角形的两直角边分别为a、b且 , 则图中大正方形的边长为 . 13. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.
13. 如图是一台多功能手机支架,图2是其侧面示意图,为地面,支架垂直地面,可分别绕点B , C转动,测量知cm,cm,cm.当转动到 , 且A , C , D三点共线时,则点A到地面的距离为cm.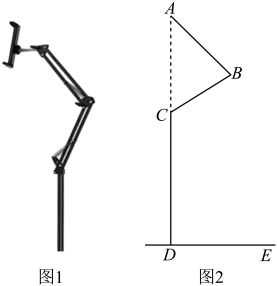
三、解答题
-
14. 如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.
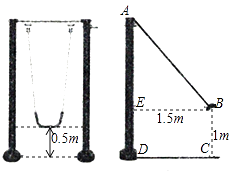
15. 材料阅读:给定三个正整数、、 , 若它们满足 , 则称、、这三个数为“勾股数”例如:, , ; , 即 , 、、这三个数为勾股数.
, , ; , 即 , 、、这三个数为勾股数.
若三角形的三条边、、满足勾股数,即 , 则这个三角形为直角三角形,且、分别为直角的两条邻边如题图所示

根据以上信息,解答下列问题:
(1)、试判断、、是否为勾股数;(2)、若某三角形的三边长分别为、、 , 求其面积;(3)、已知某直角三角形的两边长为和 , 求其周长.四、计算题
-
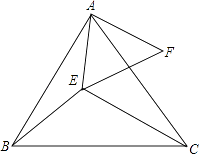
16. 如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.
五、综合题
-
17. 如图,C地到A,B两地分别有笔直的道路 , 相连,A地与B地之间有一条河流通过,A,B,C三地的距离如图所示.
 (1)、如果A地在C地的正东方向,那么B地在C地的什么方向?(2)、现计划把河水从河道 段的点D引到C地,求C,D两点间的最短距离.18. 如图 , 同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
(1)、如果A地在C地的正东方向,那么B地在C地的什么方向?(2)、现计划把河水从河道 段的点D引到C地,求C,D两点间的最短距离.18. 如图 , 同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:小明:①测量出绳子垂直落地后还剩余米,如图;
②把绳子拉直,绳子末端在地面上离旗杆底部米,如图 .
小亮:先在旗杆底端的绳子上打了一个结,然后举起绳结拉到如图点处().
 (1)、请你按小明的方案求出旗杆的高度h(米);(2)、已知小亮举起绳结离旗杆米远,此时绳结离地面多高?
(1)、请你按小明的方案求出旗杆的高度h(米);(2)、已知小亮举起绳结离旗杆米远,此时绳结离地面多高?
-