2023-2024学年人教版初中数学八年级下册17.1 勾股定理 同步分层训练培优题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 如图，是等边三角形，边长为2，根据作图的痕迹，则的长为（ ）．
A、 B、 C、 D、2. 如图，在△ABC中， ， ， 以AB，AC为边作正方形，这两个正方形的面积和为（ ）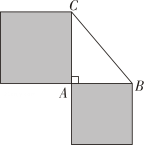
A、6 B、36 C、16 D、493. 如图，地面上有一个长方体盒子，一只蚂蚁在这个长方体盒子的顶点A处，盒子的顶点C′处有一小块糖粒，蚂蚁要沿着这个盒子的表面A处爬到C′处吃这块糖粒，已知盒子的长和宽为均为20cm，高为30cm，则蚂蚁爬行的最短距离为（ ）cm．
A、10 B、50 C、10 D、704.如图，正六边形ABCDEF中，AB=2，点P是ED的中点，连接AP，则AP的长为（ ）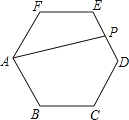
A、 B、4 C、 D、5. 如图，在Rt△OAB中，∠OAB＝90°，OA＝AB，边OA在数轴上．点A表示的数为1，以O为圆心，OA的长为半径画弧交数轴负半轴于点C，则C表示的数是( )
A、 B、 C、1 D、6. 如果梯子的底端离建筑物1.5米，2.5米长的梯子可以达到建筑物的高度是（ ）A、2米 B、2.5米 C、3米 D、3. 5米7. 如图，Rt△ABC的两条直角边BC=6，AC=8．分别以Rt△ABC的三边为边作三个正方形．若四个阴影部分面积分别为S1 ， S2 ， S3 ， S4 ， 则S2+S3-S1的值为（ ）
A、4 B、3 C、2 D、08. 如图，在Rt△ABC中，∠C＝90°，AC＝3，AB＝5，以点A为圆心，适当长为半径画弧，分别交AC ， AB于点M ， N ， 再分别以M ， N为圆心，大于的长为半径画弧，两弧在∠CAB的内部相交于点P ， 画射线AP与BC交于点D ， DE⊥AB ， 垂足为E ． 则下列结论错误的是（ ）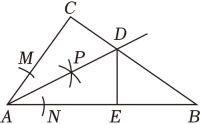
A、∠CAD＝∠BAD B、CD＝DE C、 D、二、填空题
-
9. 如图，已知Rt△ABC中，∠ACB＝90°，∠B＝30°，BC＝3，D是边AB上的一点，将△BCD沿直线CD翻折，使点B落在点B1的位置，若B1D⊥BC，则BD的长度为 ．
10. 如果直角三角形的三条边分别为3、5、 ， 那么的值等于11. 已知，如图，一轮船从港口A出发向东北方向航行了50海里，另一轮船同时从港口A出发向东南方向航行120海里，此时则两船相距海里 .
12. 等腰三角形的周长是16cm，底边长是6cm，则它的面积是13. 在中， ， ， ， 点 ， 分别是边和上的动点，始终保持 ， 连接 ， ， 则的最小值为。
14. 商场卫生间旋转门锁的局部图如图1所示，图2是其工作简化图．其中OD＝3.5cm，在自然状态下，把手竖直向下（把手底端到达A处）．旋转一定角度，使得把手底端B恰好卡在门边，此时底端A，B的竖直高度差为0.5cm，则OB的长度是 cm．当把手旋转到OC⊥OB时，点C与点B的高度差BH是 cm．
三、解答题
-
15. 已知，如图，Rt中， ， ， ， 以斜边AC为底边作等腰三角形ACD，腰AD刚好满足 ， 并作腰上的高AE．
(1)、求证：AB=AE；(2)、求等腰三角形的腰长CD．16. 如图1，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G．
(1)、求证：△ACF≌△CBG；(2)、如图2，延长CG交AB于H，连接AG交CF于点M，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；(3)、在（2）问的条件下，当∠FCH＝2∠GAC时，若BG＝4，求AM的长．四、综合题
