2023-2024学年人教版初中数学八年级下册17.1 勾股定理 同步分层训练基础题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 直角三角形的最长边的长为13，一条直角边长为5， 另一条直角边长为（ ）A、12 B、10 C、8 D、62. 如图，数轴上点A所表示的实数是（ ）
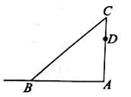
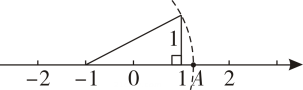A、 B、 C、 D、23. 如图，湖的两岸有A，C两点，在与AC成直角的BC方向上的点C处测得AB＝15米，BC＝12米，则A，C两点间的距离为（ ）
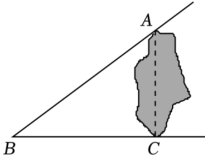A、3米 B、6米 C、9米 D、10米4. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时， 梯子底端到左墙角的距离BC为0.7m，梯子顶端到地面的距离AC为2.4m．如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A'D为1.5m，则小巷的宽为（ ）．
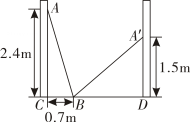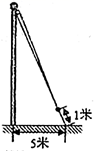
A、2.4m B、2m C、2.5m D、2.7m5. 如图，在△ABC中，∠C=90°，点D在边BC上，AD=BD，DE平分∠ADB交AB于点E．若AC=12，BC=16，则AE的长为（ ）
A、6 B、8 C、10 D、126. 如图，为了测算出学校旗杆的高度，小明将升旗的绳子拉到旗杆底端，并在与旗杆等长的地方打了一个结，然后将绳子底端拉到离旗杆底端5米的地面某处，发现此时绳子底端距离打结处约1米，则旗杆的高度是（ ）
A、12 B、13 C、15 D、247. 在Rt中， ， 则点到的距离为（ ）A、 B、 C、 D、8. 如图，是一个外轮廓为长方形的机器零件平面示意图，根据图中标注的尺寸，（单位：），可得两圆孔中心和的距离是（ ）
A、 B、 C、 D、二、填空题
-
9. Rt△ABC中，∠ACB＝90°，AB＝13，AC＝5，则BC的长为 ．10. 如图，在数轴上点A，B对应的实数分别为1，3．BC⊥AB．BC=1．以A为圆心，AC为半径画弧，交数轴正半轴于点P，则点P对应的实数为
11. 如图，在中，以A为圆心，长为半径作弧，交于C，D两点，分别以点C和点D为圆心，大于长为半径作弧，两弧交于点P，作直线 ， 交于点E，若 ， ， 则 ．
12. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm ， 则球的半径为cm.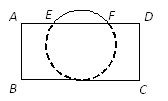
13. 如图， ， 点为平分线OC上一点，OD的垂直平分线交OA，OB分别于点P，Q，点是OA上异于点的一点，且 ， 则的面积为.
三、解答题
-
14. 若△ABC中，∠C=90°．(1)、若 ， 求；(2)、若求；15. 如图，在△ABC中，∠ACB＝90°，CE是斜边AB上的高，角平分线BD交CE于点M ．
(1)、求证：△CDM是等腰三角形．(2)、若AB＝10，AC＝8，求CM的长度．四、综合题
