2023-2024学年人教版初中数学七年级下册5.3.1 平行线的性质 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
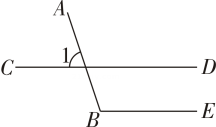
1. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )
 A、70° B、100° C、110° D、120°2. 如图,∠ACD是△ABC的外角,CE∥AB,若∠ACB=75°,∠ECD=50°,则∠A的度数为( )
A、70° B、100° C、110° D、120°2. 如图,∠ACD是△ABC的外角,CE∥AB,若∠ACB=75°,∠ECD=50°,则∠A的度数为( )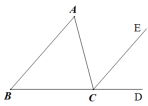 A、50° B、55° C、70° D、75°3. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A、50° B、55° C、70° D、75°3. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )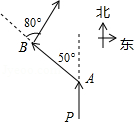 A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°4. 如图,下列结论不正确的是( )
A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°4. 如图,下列结论不正确的是( ) A、若∠2=∠C , 则AE∥CD B、若AD∥BC , 则∠1=∠B C、若AE∥CD , 则∠1+∠3=180° D、若∠1=∠2,则AD∥BC5. 如图,将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG,若 , , 根据所标数据,则的度数为( )
A、若∠2=∠C , 则AE∥CD B、若AD∥BC , 则∠1=∠B C、若AE∥CD , 则∠1+∠3=180° D、若∠1=∠2,则AD∥BC5. 如图,将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG,若 , , 根据所标数据,则的度数为( ) A、54° B、64° C、66° D、72°6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
A、54° B、64° C、66° D、72°6. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )已知:如图, , , 垂足为D , F , .
求证: .
证明:∵ , ,
∴ ◎ ,
∴(同位角相等,两直线平行),
∴ @ (两直线平行,同旁内角互补).
又∵ ,
∴ ▲ (同角的补角相等),
∴( ※ 相等,两直线平行).
 A、◎代表 B、@代表 C、▲代表 D、※代表同位角7. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A、◎代表 B、@代表 C、▲代表 D、※代表同位角7. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )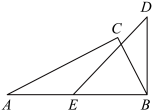 A、或或 B、或或 C、或或 D、或或8. 将一副三角板如图放置,则下列结论中,正确的是( )
A、或或 B、或或 C、或或 D、或或8. 将一副三角板如图放置,则下列结论中,正确的是( )①;②如果 , 则有;③如果 , 则有;④如果 , 则有 .
 A、①②③④ B、③④ C、①②④ D、①②③
A、①②③④ B、③④ C、①②④ D、①②③二、填空题
-
9. 如图,∠BAF=46°,∠ACE=136°.CE⊥CD,则CD与AB平行的(填“是”或“不是”).
 10. 将一副三角尺和一张对边平行的纸条按如图所示的方式摆放,两块三角尺的一条直角边重合,含30°角的三角尺的斜边与纸条的一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是
10. 将一副三角尺和一张对边平行的纸条按如图所示的方式摆放,两块三角尺的一条直角边重合,含30°角的三角尺的斜边与纸条的一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是 11. 如图,若∠1+∠2=240°,b∥c,则∠3=.
11. 如图,若∠1+∠2=240°,b∥c,则∠3=. 12. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)
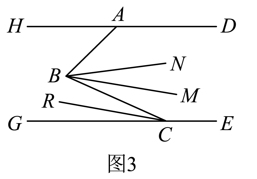
12. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)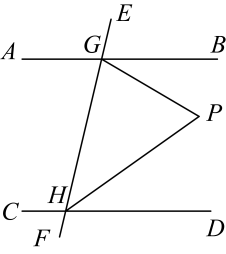 13. 如图
13. 如图 (1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .
(1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .三、解答题
-
14. 如图,AB∥CD,BO与CD相交于点O,OE⊥BO,OF平分∠BOD.若∠ABO=50°,求∠EOF的度数.
 15. 探究三角形的内角和(1)、下面是证明三角形内角和定理的一种添加辅助线的方法,请完成证明.
15. 探究三角形的内角和(1)、下面是证明三角形内角和定理的一种添加辅助线的方法,请完成证明.三角形的内角和定理:三角形的内角和等于180°.

已知:如图,△ABC
求证:∠A+∠B+∠C=180°
证明:在BC上任取一点D,过点D作DE∥AB,交AC于点E,过点D作DF∥AC,交AB于点F.
(2)、请再用一种不同的方法证明三角形内角和定理.四、作图题
-
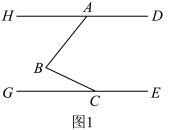
16. 线段 , 交于点 , 为直线上一点(不与点 , 重合).过点在的右侧作射线 , 过点作直线 , 交于点(与不重合).(1)、如图1,若点在线段上,且为钝角.
①按要求补全图形;
②判断与的数量关系,并证明.
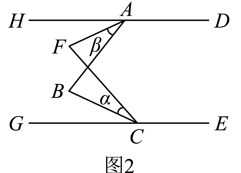
 (2)、若点在线段的延长线上,请直接写出与的数量关系
(2)、若点在线段的延长线上,请直接写出与的数量关系
五、综合题