2023-2024学年人教版初中数学七年级下册5.3.1 平行线的性质 同步分层训练提升题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 如图，已知l1∥l2 ， ∠1=50°，则∠2等于（ ）
A、135° B、130° C、50° D、40°2. 如果两条直线被第三条直线所截，那么（ ）A、同位角相等 B、内错角相等 C、同旁内角互补 D、对顶角相等3. 将一直角三角板与两边平行的纸条如图所示放置，若∠1=55°，则∠2的度数为（ ）
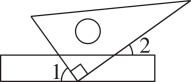A、135° B、130° C、45° D、35°4. 如图，平分 ， 求证：.以下是排乱的证明过程：
①(已知)，
②平分(已知)，
③(角平分线的定义)，
④(两直线平行，同位角相等)，
⑤(等量代换).
证明步㵵顺序正确的是（ ）
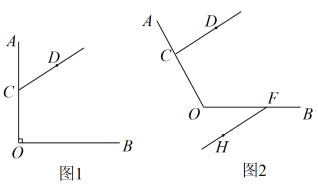
A、③②①④⑤ B、①④②③⑤ C、①③④②⑤ D、①④③②⑤5. 如图，一条街道有两个拐角和 ， 已知 ， 若 ， 则的度数是（ ）
A、30° B、120° C、130° D、150°6. 如图，已知AB∥EF．若∠C=90°，则∠α，∠β，∠γ之间的关系是（ ）
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°7. 一把直尺与一块直角三角板按如图方式摆放，若∠1=46°，则∠2=（ ）
A、46° B、44° C、42° D、40°8. 生活中常见的探照灯、汽车大灯等灯具都与抛物线有关。如图，从光源P点照射到抛物线上的光线PA，PB等反射以后沿着与直线PF平行的方向射出，若∠CAP=α，∠DBP=β，则∠APB的度数为（ ）
A、2α B、2β C、α+β D、(α+β)二、填空题
-
9. 如图，l1∥l2 ， 直线AB截l1于点A，截l2于点B，BC⊥AB，若∠1=30°，则∠2=°
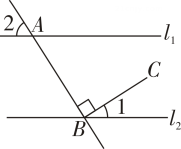10. 如图，已知∠1=60°，∠2=58°，∠3=60°，则∠4= ．
11. 如图，在三角形ABC中，D，E，F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°，则∠EFD的度数为.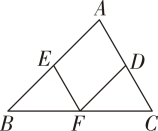
12. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=49°，则∠2﹣∠1= ．
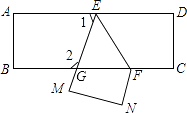13. 如图， ， 在的两边上分别过点A和点C向同方向作射线和 ， 且 ， 若和的角平分线所在的直线交于点P（P与C不重合），则的大小为 ．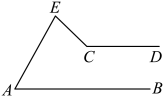
三、解答题
-
14. 如图，AB∥CD，CB平分∠ACD，∠A=50°，求∠B的度数．
15. 如图，已知∠EPM=∠FQM．∠AEP=∠CFQ．试说明AB∥CD的理由．
四、作图题
-
16. 如图， ． 【友情提示：尺规作图要用圆规，并保留痕迹；画完图要写完整结论】
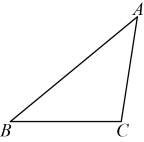(1)、尺规作图：在上取一点 ， 使；(2)、画图：过点画直线交于点；(3)、在（1）（2）的条件下，连接 ， 若 ， 求的度数．五、综合题
