2023-2024学年人教版初中数学七年级下册5.3.1 平行线的性质 同步分层训练基础题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 已知直线 m∥n.将一把含30°角的三角尺ABC按如图所示的方式放置(∠ABC=30°),其中A、B两点分别落在直线m、n上.若∠1=20°,则∠2的度数为( )
 A、10° B、20° C、30° D、40°2. 如图,直线 , 被直线所截, , , 则的度数为( )
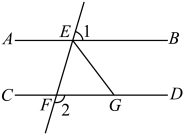
A、10° B、20° C、30° D、40°2. 如图,直线 , 被直线所截, , , 则的度数为( ) A、 B、 C、 D、3. 如图,已知AB∥CD,则图中与∠1相等的角有( )
A、 B、 C、 D、3. 如图,已知AB∥CD,则图中与∠1相等的角有( )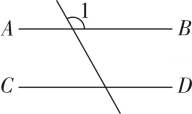 A、5个 B、4个 C、3个 D、2个4. 下列图形中,由 , 能得到的是( )A、
A、5个 B、4个 C、3个 D、2个4. 下列图形中,由 , 能得到的是( )A、 B、
B、 C、
C、 D、
D、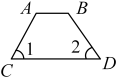 5. 如图,直线 , 是直角三角形, , 点在直线上若 , 则的度数是( )
5. 如图,直线 , 是直角三角形, , 点在直线上若 , 则的度数是( ) A、 B、 C、 D、6. 下列推理中错误的是( )A、因为AB=CD,CD=EF,所以AB=EF B、因为所以 C、因为所以a∥c D、因为所以7. 如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
A、 B、 C、 D、6. 下列推理中错误的是( )A、因为AB=CD,CD=EF,所以AB=EF B、因为所以 C、因为所以a∥c D、因为所以7. 如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )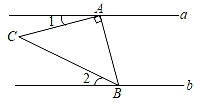 A、40° B、45° C、50° D、55°8. 如图,直线 , 是直角三角形, , 点C在直线n上.若 , 则的度数是( )
A、40° B、45° C、50° D、55°8. 如图,直线 , 是直角三角形, , 点C在直线n上.若 , 则的度数是( ) A、60° B、50° C、45° D、40°
A、60° B、50° C、45° D、40°二、填空题
-
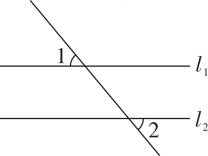
9. 如图,直线l1∥l2 . 若∠1=52°,则∠2的度数为
 10. 如图,由AB∥CD,可得∠B+=180°,理由是
10. 如图,由AB∥CD,可得∠B+=180°,理由是 11. 一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.
11. 一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.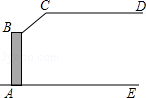 12. 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,则∠2=.
12. 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,则∠2=. 13. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
13. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
三、解答题
-
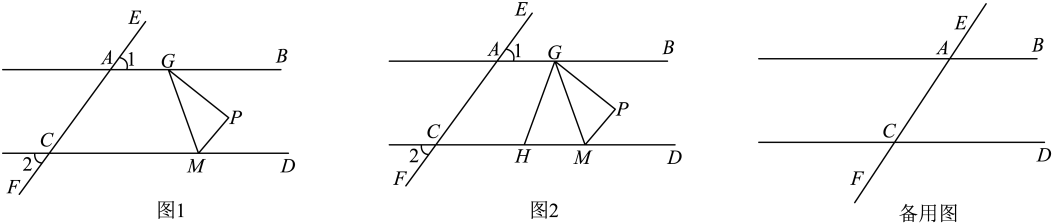
14. 如图,已知∠1=∠2=∠A.
 (1)、试说明∠1=∠3的理由.(2)、当∠ADG=80°时,求∠2的度数.15. 如图①.在四边形ABCD中.∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)、试说明∠1=∠3的理由.(2)、当∠ADG=80°时,求∠2的度数.15. 如图①.在四边形ABCD中.∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余. (1)、试判断直线BE与DF的位置关系.并说明理由.(2)、如图②,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为H.试判断∠FBH与∠GBH的大小关系,并说明理由.
(1)、试判断直线BE与DF的位置关系.并说明理由.(2)、如图②,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为H.试判断∠FBH与∠GBH的大小关系,并说明理由.四、综合题