2023-2024学年人教版初中数学七年级下册5.2.2 平行线的判定 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1.
如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
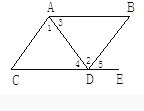 A、∠1=∠2 B、∠3=∠4 C、∠5=∠B D、∠B+∠BDC=180°2. 如图,下列条件中,能判定的是( )
A、∠1=∠2 B、∠3=∠4 C、∠5=∠B D、∠B+∠BDC=180°2. 如图,下列条件中,能判定的是( )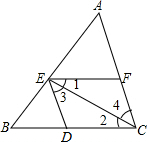 A、 B、 C、 D、3. 如图,能判定的是( )
A、 B、 C、 D、3. 如图,能判定的是( )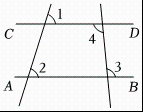 A、 B、 C、 D、4. 如图,点E在的延长线上,下列条件中能判断的是( )
A、 B、 C、 D、4. 如图,点E在的延长线上,下列条件中能判断的是( ) A、 B、 C、 D、5. 如图,下列条件中:(1);(2);(3);(4) . 能判定的条件个数有( )
A、 B、 C、 D、5. 如图,下列条件中:(1);(2);(3);(4) . 能判定的条件个数有( )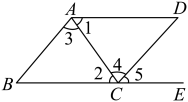 A、1个 B、2个 C、3个 D、4个6. 如图,下列推理不正确的是( )
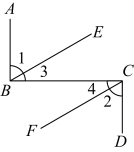
A、1个 B、2个 C、3个 D、4个6. 如图,下列推理不正确的是( ) A、 , B、 , C、 , D、 ,7. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .
A、 , B、 , C、 , D、 ,7. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .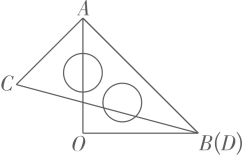 A、 B、或 C、或 D、或8. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A、 B、或 C、或 D、或8. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )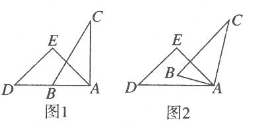 A、 和 B、 和 C、 和 D、以上都有可能
A、 和 B、 和 C、 和 D、以上都有可能二、填空题
-
9. 在平面内,若 , , 则 .10. 如图,点D,E,F分别是△ABC的边AB,AC,BC上的点.
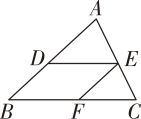
若∠B= , 则EF∥AB;
若∠B= , 则DE∥BC.
11. 如图,直线a∥b , 直线c与直线a , b分别交于点A , B . 若∠1=45°,则∠2= . 12. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.
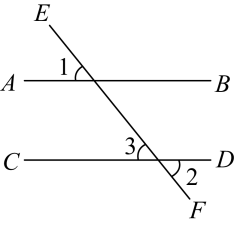
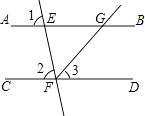
12. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.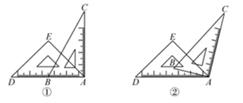 13. 如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
13. 如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.解:因为∠1=∠2=80°(已知),
所以AB∥CD()
所以∠BGF+∠3=180°()
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD= . (等式性质).
因为FG平分∠EFD(已知).
所以∠3=∠EFD(角平分线的性质).
所以∠3= . (等式性质).
所以∠BGF= . (等式性质).
三、解答题
-
14. 已知:如图, , , , , 求证: .
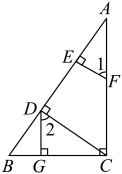
证明:∵ , (已知)
∴ , (垂直定义)
∴
∴( )
∴ ▲ ( )
∵(已知)
∴ ▲ (等量代换)
∴( )
∴ ▲ ( )
∵(已知)
∴(垂直定义)
∴ ▲ (等量代换)
∴(垂直定义)
四、综合题