2023-2024学年人教版初中数学七年级下册5.2.1 平行线 同步分层训练培优题
试卷更新日期:2024-01-20 类型:同步测试
一、选择题
-
1. 如图,工人师傅用角尺画出工件边缘 的垂线 和 ,得到 理由是( )
 A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行
A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行 -
2. 下列尺规作图不能得到平行线的是( )A、
 B、
B、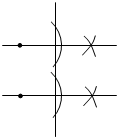 C、
C、 D、
D、
-
3. 下列命题中:①有公共顶点和一条公共边的两个角一定是邻补角;②垂直于同一条直线的两条直线互相垂直;③相等的角是对顶角;④经过直线外一点,有且只有一条直线与已知直线平行;其中真命题的个数是( )A、0个 B、1个 C、2个 D、3个
-
4. 若直线a,b,c,d有下列关系,则推理正确的是( )A、∵ , ,
∴
B、∵ , ,∴
C、∵ , ,∴
D、∵ , ,∴
-
5. 下列说法正确的是( )
①在同一平面内,过一点有且只有一条直线与已知直线垂直;
②在同一平面内,过一点有且只有一条直线与已知直线平行;
③ 是直线 外一点, 、 、 分别是直线 上的三点, , , ,则点 到直线 的距离一定是1;
④相等的角是对顶角;
⑤同旁内角互补.
A、1个 B、2个 C、3个 D、4个 -
6. 已知直线 及直线 外一点 ,要求利用尺规作图过 点作直线 的平行线.对如图所示的两种作法,下列说法正确的是( )
 A、两种作法都正确 B、两种作法都错误 C、左边作法正确,右边作法错误 D、右边作法正确,左边作法错误
A、两种作法都正确 B、两种作法都错误 C、左边作法正确,右边作法错误 D、右边作法正确,左边作法错误 -
7. 如图,笔直的公路一旁是电线杆,若其余电线杆都与电线杆①平行,则判断其余电线杆两两平行的根据是( )
 A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、同旁内角互补,两直线平行 D、平行于同一条直线的两条直线平行
A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、同旁内角互补,两直线平行 D、平行于同一条直线的两条直线平行 -
8. 下面给出的四个语句,其中正确的有( )
①等角的余角相等;
②一个角的补角一定大于这个角;
③有理数分为正数和负数;
④零是最小的正数;
⑤过直线外一点可以作一条以上的直线与已知直线平行.
A、1个 B、2个 C、3个 D、4个
二、填空题
-
9. 张老师出了一道题目“若PC∥AB,QC∥AB.则点P,C,Q在一条直线上”,点点答出了其中的理由,你认为点点的回答是:。
-
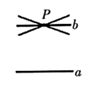
10. 如图,在直线a外有一点P,经过点P可以画无数条直线,如果 ,那么过点P的其它直线与直线a一定不平行,理由是 .
-
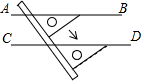
11. 如图,利用三角尺和直尺可以准确的画出直线AB∥CD,下面是某位同学弄乱了顺序的操作步骤:
①沿三角尺的边作出直线CD;
②用直尺紧靠三角尺的另一条边;
③作直线AB,并用三角尺的一条边贴住直线AB;
④沿直尺下移三角尺;正确的操作顺序应是: .
-
12. 如果∠ 与∠ 的两条边分别平行,其中∠ = °;∠ = °,则∠ 的度数为
三、解答题
-
13.
如图点P是∠ABC内一点画图:
①过点P作BC的垂线,D是垂足;
②过点P作BC的平行线交AB于E,过点P作AB的平行线交BC于F.

-
14.
如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?

四、作图题
-
15. 根据下列要求画图:(1)、如图,

点A, B,C分别表示某公园平地上的三棵树,藏宝的地点D与这三棵树恰好构成一个平行四边形,请在图中作出所有可能的藏宝地点D的位置.
(2)、如图,已知点P和∠ABC,以点P为顶点画∠DPE,使得PD∥ BA,PE∥ BC,然用量角器量得:∠ABC=°,∠DPE=°,并猜想∠DPE与∠ABC的关系为 .
五、综合题
-
16. 如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
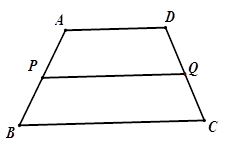 (1)、PQ与BC平行吗?为什么?(2)、测DQ与CQ的长,DQ与CQ是否相等?
(1)、PQ与BC平行吗?为什么?(2)、测DQ与CQ的长,DQ与CQ是否相等? -
17. 课题学习:平行线的“等角转化”功能.
 (1)、阅读理解:如图1,已知点A是外一点,连接、 , 求的度数.阅读并补充下面推理过程.
(1)、阅读理解:如图1,已知点A是外一点,连接、 , 求的度数.阅读并补充下面推理过程.解:过点A作 ,

▲ , ▲ ,
,
.
(2)、方法运用:如图2,已知 , 求的度数;(3)、深化拓展:已知 , 点C在点D的右侧, , 平分 , 平分 , , 所在的直线交于点E,点E在直线与之间.①如图3,点B在点A的左侧,若 , 求的度数.
②如图4,点B在点A的右侧,且 , .若 , 求度数.(用含n的代数式表示)
