2023-2024学年人教版初中数学七年级下册5.1.3 同位角、内错角、同旁内角 同步分层训练培优题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 如图所示，下列说法中错误的是（ ）
A、∠2与∠B是内错角 B、∠A与∠1是内错角 C、∠3与∠B是同旁内角 D、∠A与∠3是同位角2. 下列四个图形中，与互为内错角的是（ ）A、
B、
C、
D、
3. 如图，AB∥CD，点E在BC上，DE⊥BC，∠B=40°，则∠D的度数为（ ）
A、40° B、50° C、38° D、60°4. 如图，下列说法中，错误的是（ ）
A、∠3和∠4是邻补角 B、∠1和∠2是同旁内角 C、∠1和∠5是同位角 D、∠5和∠6是内错角5. 中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金，这是她获得的首个冬奥会奖牌，也是中国运动员第一次参加冬奥会大跳台的比赛．项目图标如下图；则在下列判断中①∠1与∠2是对顶角；②∠3与∠4是同旁内角；③∠5与∠6是同旁内角；④∠1与∠4是内错角，其中正确的有（ ）个．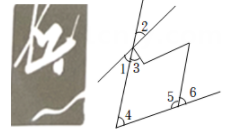
A、1 B、2 C、3 D、46. 如图所示，下列三幅图依次是两只手的食指和拇指在同一平面内所构成的角，依次表示（ ）
A、同位角，同旁内角、内错角 B、同位角、内 错角、同旁内角 C、同位角、对顶角．同旁内角 D、同位角、内错角、对顶角7. 如图，直线ABCD，且AC⊥CB于点C，若∠BCD＝55°，则∠BAC的度数为（ ）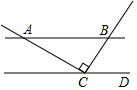
A、65° B、55° C、45° D、35°8. 如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有 ( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图，于点E，交于点 ， 已知 ， 则的度数为 ．
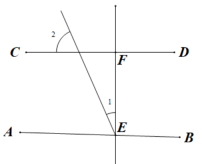10. 如图，若使∠1=∠2，则需添加哪两条直线平行
11. 如图，直线、被直线所截，交点分别为M、N，则的同位角是.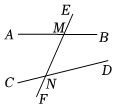
12. 如图，直线 ， 被所截，则与是填内错角，同位角或同旁内角.
13. 如图，“4”字图中有a对同位角，b对内错角，c对同旁内角，则abc= ．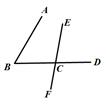
三、解答题
-
14. 如图，直线AD与AE相交于点A，直线BC分别交AD、AE于点B、C，直线DE分别交AD、AE于点D、E，分别写出图中的两对同位角、两对内错角、两对同旁内角．
15. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．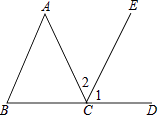
四、综合题
-
16. 【概念认识】
两条直线相交所形成的锐角或直角称为这两条直线的夹角，如果两条直线的夹角为α，那么我们称这两条直线是“α相交线”例如；如图①，直线m和直线n为“α相交线”我们已经知道两条平行线被第三条直线所截，同位角相等、内错角相等、同旁内角互补，那么若两条直线为“α相交线”，它们被第三条直线所截后形成的同位角、内错角、同旁内角之间有什么关系呢？
(1)、【初步研究】如图②，直线m与直线n是“α相交线”，求证：
小明的证法如图③．若直线m与直线n交于点O，
直线m与直线n是“α相交线”．
∵ ．
∴是的外角，
∴ ．
即 ．
请补充完整小明的证明过程，并用另一种不同的方法进行证明
(2)、【深入思考】如图④，直线m与直线n是α相交线，
①找出直线m与直线n被直线l所截得的内错角，并直接写出内错角与α的关系；
②找出直线m与直线n被直线l所截得的同旁内角，并直接写出每对同旁内角与α的关系；
(3)、【综合运用】如图⑤，已知∠α，用直尺和圆规按下列要求作图，
如图⑥，直线外求作一点M，使得直线与直线是“α相交线”（不写作图过程，保留作图痕迹）．
17. 复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．
(1)、如图1，直线 ， 被直线 所截，在这个基本图形中，形成了对同旁内角．(2)、如图2，平面内三条直线 ， ， 两两相交，交点分别为A、B、C，图中一共有对同旁内角．(3)、平面内四条直线两两相交，最多可以形成对同旁内角．(4)、平面内n条直线两两相交，最多可以形成对同旁内角．