2023-2024学年人教版初中数学七年级下册5.1.2 垂线 同步分层训练提升题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
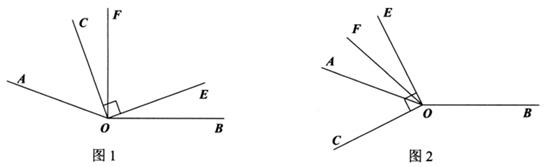
1. 如图，是直线外一点，是线段的中点，连接 ， 过点作 ， 垂足为点 ， 则点到直线的距离是（ ）
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度2. 如图，点D为直线上一点，于点D ， ． 点P是直线上的一个动点，则线段的长度可能是（ ）．
A、10 B、7 C、5 D、43. 如图，点在直线上，若 ， 则等于（ ）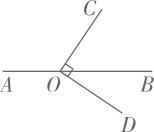
A. A、 B、 C、4. 如图，斑马线的作用是为了引导行人安全地通过马路，小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（ ）
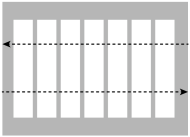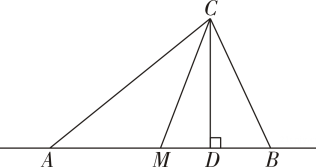
A、垂线段最短 B、过直线外一点有且只有一条直线与已知直线平行 C、两点确定一条直线 D、两点之间，线段最短5. 如图是小林同学一次立定跳远的示意图，小林从点A起跳，落在点B处，经测盘，米，那么小林实际的跳远成绩可能是（ ）米．
A、2.10 B、2.35 C、2.41 D、2.566. 如图，直线公路l上共有A、B、C、D四个核酸检测点，若从点M用相同速度到任意一个核酸检测点，用时最短的路径是（ ）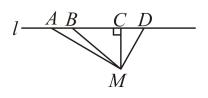
A、 B、 C、 D、7. 如图，已知 ， 垂足为点 ， 图中与的关系是（ ）
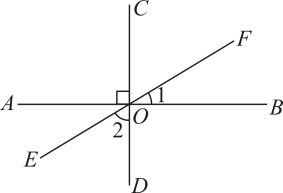A、 B、 C、 D、无法确定8. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（ ）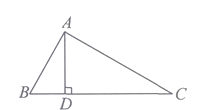
①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
⑥AD+BD>AB．
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 已知：如图，直线BO⊥AO于点O，OB平分∠COD，∠BOD＝22°．则∠AOC的度数是 度．
10. 如图所示，要在河的两岸搭建一座桥，沿线段搭建最短，理由是 ．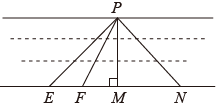
11. 已知∠A与∠B的两边互相垂直，且2∠A-∠B＝30°，则∠A的度数为 ．12. 如图，直线AB和CD交于点O，EO⊥AB，垂足为O，∠AOD＝125°，则∠COE＝°．
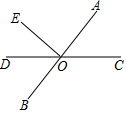13. 如图，点O在直线上，过点O作射线 ， ， ． 从下面的四个条件中任选两个，可以推出的是（写出一组满足题意的序号）．①；②和互余；③；④ ．
三、解答题
-
14. 如图，已知直线AB与CD相交于点O，EO⊥CD于点O，OF平分∠AOD，且∠BOE=50°，求∠COF的度数.
15. 如图，直线相交于点O ， ， ． 求与的度数．
四、作图题
-
16. 如图，在中， ， 请用尺规作图法在边AB上找一点P，使得CP的长最小．（保留作图痕迹，不写作法）
五、综合题
