2023-2024学年人教版初中数学七年级下册5.1.1 相交线 同步分层训练提升题
试卷更新日期：2024-01-20 类型：同步测试
一、选择题
-
1. 下列四个图形中，与是邻补角的是（ ）A、
B、
C、
D、
2. 如图，直线AC和直线BD相交于点O，若∠1＋∠2＝70°，则∠BOC的度数是（ ）．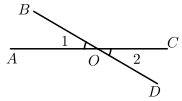
A、100° B、115° C、135° D、145°3. 下面四个图形中，∠1与∠2是对顶角的图形是（ ）A、
B、
C、
D、
4. 如图，若相交于点O ， 过点O作 ， 则下列结论不正确的是（ ）
A、与互为余角 B、与互为余角 C、与是对顶角 D、与是邻补角5. 如图， ， 点 ， ， 在同一直线上，若 ， 则的度数为（ ）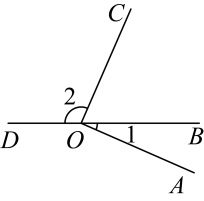
A、113° B、 C、 D、6. 如图，直线a，b相交， ， 则的度数为（ ）
A、 B、 C、 D、7. 已知：如图， ， 垂足为 ， 为过点的一条直线，则与的关系一定成立的是（ ）
A、相等 B、互余 C、互补 D、互为对顶角8. 用一个平面去截一个正方体所得的截面的边数最多是（ ）A、4 B、3 C、6 D、5二、填空题
-
9. 如图，直线、、相交于点 ， 其中 ， ， 则 ．
10. 如图，与是对顶角， ， ， 则°．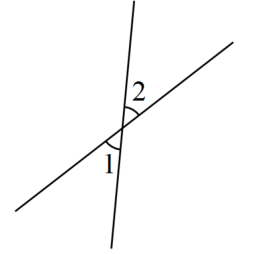
11. 直线 ， 相交于点 ， ， 则直线 ， 的夹角是 ．12. 如图，已知直线AB与直线CD交于点O，∠BOC＝45°，若 ， 则∠DOE＝ ．
13. 为了测量一座古塔外墙底部的底角∠AOB的度数，李潇同学设计了如下测量方案：分别作AO，BO的延长线OD，OC，量出∠COD的度数，从而得到∠AOB的度数．这个测量方案的依据是
14. 如图，将一副三角尺按不同的位置摆放，∠α与∠β一定相等的图形有(填序号)
三、解答题
-
15. 如图，三条直线AB、CD、EF相交于点O，若∠3＝3∠2、∠2＝2∠1，求∠1、∠2、∠3的度数.
16. 已知：点为直线上一点，过点作射线 ， ．
(1)、如图1，求的度数；(2)、如图2，过点作射线 ， 使 ， 作的平分线 ， 求的度数；(3)、如图3，在（2）的条件下，作射线 ， 若与互余，请画出图形，并求的度数．四、综合题
