【培优卷】2024年浙教版数学八年级下册2.3 一元二次方程的应用同步练习
试卷更新日期:2024-01-19 类型:同步测试
一、单选题
-
1. 某超市销售一种商品,其进价为每千克30元,按每千克45元出售,每天可售出300千克,为让利于民,超市采取降价措施,当售价每千克降低1元时,每天销量可增加50千克,若每天的利润要达到5500元,则实际售价应定为多少元?设售价每千克降低x元,可列方程为( )A、(45-30-x)(300+50x)=5500 B、(x-30)(300+50x)=5500 C、(x-30)[300+50(x-45)]=5500 D、(45-x)(300+50x)=55002. 对于一元二次方程,我国及其他一些国家的古代数学家还研究过其几何解法呢!以方程x2+2x﹣35=0即x(x+2)=35为例加以说明,三国时期的数学家赵爽在其所著的《勾股圆图注》中记载的方法是:构造如图,一方面,图中的大方形的面积是(x+x+2)2;另一方面,它又等于四个矩形面积加上中间小正方形的面积,即4×35+22,据此易得x=5,那么在下面的四个构图中,能够说明x2﹣2x﹣8=0的正确构图是( )
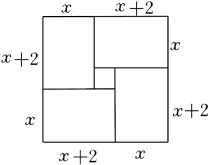 A、
A、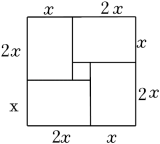 B、
B、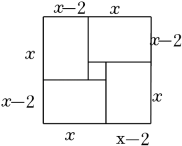 C、
C、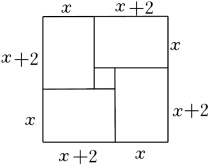 D、
D、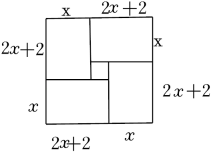 3. 我国古代数学家研究过一元二次方程的正数解的几何解法以方程 , 即为例说明,方图注中记载的方法是:构造如图中大正方形的面积是同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此小明用此方法解关于的方程时,构造出同样的图形,已知大正方形的面积为 , 小正方形的面积为 , 则( )
3. 我国古代数学家研究过一元二次方程的正数解的几何解法以方程 , 即为例说明,方图注中记载的方法是:构造如图中大正方形的面积是同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 因此小明用此方法解关于的方程时,构造出同样的图形,已知大正方形的面积为 , 小正方形的面积为 , 则( )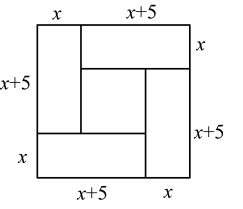 A、 , B、 , C、 , D、 ,4. 如图,将图1的正方形剪成四块,恰能拼成图2的矩形,则的值为( )
A、 , B、 , C、 , D、 ,4. 如图,将图1的正方形剪成四块,恰能拼成图2的矩形,则的值为( )
 A、 B、 C、 D、+1
A、 B、 C、 D、+1二、填空题
-
5. 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,则第二周每个旅游纪念品的销售价格为元.
6. 为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对原有的小麦品种进行改良种植研究.在保持去年种植面积不变的情况下,今年预计小麦平均亩产量将在去年的基础上增加a%,因为优化了品种,预计每千克售价将在去年的基础上上涨2a%,全部售出后预计总收入将增加68%,则a的值为 .7. 一个两位数,十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调,得到的两位数比原来的两位数小27,则原来的两位数是8. 有学者认为,阿拉伯数学家花拉子米的《代数学》关于一元二次方程的几何求解法与中国古代数学的“出入相补原理”相近,可能受到中国传统数学思想的影响,花拉子米关于的几何求解方法如图1,在边长为x的正方形的四个边上向外做边长为x和的矩形,再把它补充成一个边长为的大正方形,我们得到大正方形的面积为(因为).所以大正方形边长为 , 得到 . 思考:当我们用这种方法寻找的解时,如图2中间小正方形的边长x为;阴影部分每个正方形的边长为 .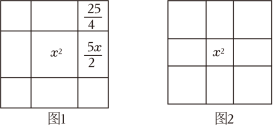
三、综合题
-
9. 在新冠肺炎流行中,某商家预测库存的带防护面罩的遮阳帕将能畅销市场预计平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,回笼资金,商场决定采取适当的降价措施,经调查发现,如果每个遮阳帽每降价1元,商场平均每天可多售出2个,若商场平均每天要赢利1200元,每个遮阳帽应降价多少元?10. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其他两位成员交流的情况.
小张:“该商品的进价为24元/件.”
成员甲:“当定价为40元/件时,每天可售出480件.”
成员乙:“若单价每涨1元,则每天少售出20件;若单价每降1元,则每天多售出40件.”根据他们的对话,请你求出要使该商品每天获利7680元,应该怎样合理定价?
11. 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6CM.点P,Q同时由B,A两点出发,分别沿射线BC,AC方向以1cm/s的速度匀速运动. (1)、几秒后△PCQ的面积是△ABC面积的一半?(2)、连结BQ,几秒后△BPQ是等腰三角形?12. 如图,在直角梯形中, , , , , . 动点从点出发,沿射线的方向以每秒2个单位的速度运动,动点从点出发,沿射线的方向以每秒1个单位的速度向点运动,点 , 分别从点 , 同时出发,当点运动到点时,点随之停止运动.设运动的时间为(秒),当为何值时,以 , , 三点为顶点的三角形是等腰三角形?
(1)、几秒后△PCQ的面积是△ABC面积的一半?(2)、连结BQ,几秒后△BPQ是等腰三角形?12. 如图,在直角梯形中, , , , , . 动点从点出发,沿射线的方向以每秒2个单位的速度运动,动点从点出发,沿射线的方向以每秒1个单位的速度向点运动,点 , 分别从点 , 同时出发,当点运动到点时,点随之停止运动.设运动的时间为(秒),当为何值时,以 , , 三点为顶点的三角形是等腰三角形?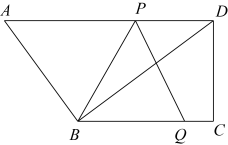 13. 某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示.
13. 某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示. (1)、求y与x之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?14. 我市大力发展经济作物,其中果树种植己初具规模,但是今年受气候、雨水等因素的影响,“开心农场”里的蓝莓较去年有所减产,而黄桃却有所增产.(1)、该农场今年收获蓝莓和黄桃共500千克,其中黄桃的产量不超过蓝莓产量的4倍,求该农场今年收获蓝莓至少多少千克?(2)、该农场把今年收获的蓝莓和黄桃两种水果的一部分运往市场销售,已知去年蓝莓的市场销售量为300千克,销售均价为50元/千克,黄桃的市场销售量为600千克,销售均价为30元千克,今年蓝莓的市场销售量比去年减少了 , 销售均价比去年提高10元/千克,黄桃的市场销售量比去年增加了 , 但销售均价比去年减少了 . 农场今年蓝莓和黄桃的市场销售总金额比去年蓝莓和黄桃的市场销售总金额少6000元,求p的值.15. 2019年小王看中了某楼盘以12000元每平方米的均价对外销售面积为100平方米的某户型,由于资金不足,决定等两年再考虑买房.自2019年底出现疫情以来,商品房价格下调,2021年的该户型的均价为9720元每平方米 .(1)、求这一户型的均价平均每年下调的百分率;(2)、进入2022年后小王得知该户型仍有少量库存在售,单价较2021年的均价再次下调相同的百分率.小王计算了一下自己的资金,在过去的24个月中,每月固定存相相同数量的资金(存入的资金是100的整数倍),加上原有积蓄30万元,还可以向银行贷款50万元,可以凑齐房款,请问小王在过去的两年中每月至少固定存入多少钱?16. 如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)、求y与x之间的函数关系式;(2)、商贸公司要想获利2090元,则这种干果每千克应降价多少元?14. 我市大力发展经济作物,其中果树种植己初具规模,但是今年受气候、雨水等因素的影响,“开心农场”里的蓝莓较去年有所减产,而黄桃却有所增产.(1)、该农场今年收获蓝莓和黄桃共500千克,其中黄桃的产量不超过蓝莓产量的4倍,求该农场今年收获蓝莓至少多少千克?(2)、该农场把今年收获的蓝莓和黄桃两种水果的一部分运往市场销售,已知去年蓝莓的市场销售量为300千克,销售均价为50元/千克,黄桃的市场销售量为600千克,销售均价为30元千克,今年蓝莓的市场销售量比去年减少了 , 销售均价比去年提高10元/千克,黄桃的市场销售量比去年增加了 , 但销售均价比去年减少了 . 农场今年蓝莓和黄桃的市场销售总金额比去年蓝莓和黄桃的市场销售总金额少6000元,求p的值.15. 2019年小王看中了某楼盘以12000元每平方米的均价对外销售面积为100平方米的某户型,由于资金不足,决定等两年再考虑买房.自2019年底出现疫情以来,商品房价格下调,2021年的该户型的均价为9720元每平方米 .(1)、求这一户型的均价平均每年下调的百分率;(2)、进入2022年后小王得知该户型仍有少量库存在售,单价较2021年的均价再次下调相同的百分率.小王计算了一下自己的资金,在过去的24个月中,每月固定存相相同数量的资金(存入的资金是100的整数倍),加上原有积蓄30万元,还可以向银行贷款50万元,可以凑齐房款,请问小王在过去的两年中每月至少固定存入多少钱?16. 如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求: (1)、经过6秒后,BP=cm,BQ=cm;(2)、经过几秒后,△BPQ是直角三角形?(3)、经过几秒△BPQ的面积等于 cm2?17. 已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
(1)、经过6秒后,BP=cm,BQ=cm;(2)、经过几秒后,△BPQ是直角三角形?(3)、经过几秒△BPQ的面积等于 cm2?17. 已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: (1)、经过 秒时,求△PBQ的面积;(2)、当t为何值时,△PBQ是直角三角形?(3)、是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
(1)、经过 秒时,求△PBQ的面积;(2)、当t为何值时,△PBQ是直角三角形?(3)、是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.