湖南省长沙市明德教育集团2023-2024学年九年级上学期月考数学试题

试卷更新日期：2024-01-19 类型：月考试卷

进入出卷网下载

一、选择题（在下列各题的四个选项中，只有一项是正确答案，请在答题卡中填涂符合题意的选项．本大题共10个小题，每小题3分，共30分）

1. 下列图案中，可以看作中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知⊙O的半径为4，点O到直线m的距离为3，则直线m与⊙O公共点的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 已知 $x = 1$ 是方程 $x^{2} - 2 x + c = 0$ 的一个根，则实数c的值是（　　）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
4. 把二次函数y＝3x²的图象向右平移2个单位，再向下平移1个单位，所得到的图象对应的二次函数表达式是（　　）

A、y＝3（x+2）²+1 B、y＝3（x+2）²﹣1 C、y＝3（x﹣2）²﹣1 D、y＝3（x﹣2）²+1

查看试题解析
5. 如图，在 $⊙ O$ 中， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ， $∠ B = 70 °$ ，则 $∠ A$ 的度数为（）

A、 $20 °$ B、 $40 °$ C、 $70 °$ D、 $110 °$

查看试题解析
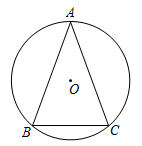6. 二次函数 $y = k x^{2} - 6 x + 3$ 的图象与x轴有交点，则k的取值范围是（）

A、 $k < 3$ B、 $k < 3$ 且 $k \neq 0$ C、 $k \leq 3$ D、 $k \leq 3$ 且 $k \neq 0$

查看试题解析
7. 如图，已知Rt△ABC中，∠C＝90°，AC＝8，BC＝15，则tanA的值为(　　)

A、 $\frac{8}{17}$ B、 $\frac{15}{17}$ C、 $\frac{8}{15}$ D、 $\frac{15}{8}$

查看试题解析
8. 若点 $A (- 5 ， y_{1}) ， B (1 ， y_{2}) ， C (5 ， y_{3})$ 都在反比例函数 $y = - \frac{5}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
9. 如图，在 $Δ A B C$ 中，点 $D ， E ， F$ 分别是边 $A B ， A C ， B C$ 上的点， $D E ∥ B C ， E F ∥ A B$ ，且 $A D ： D B = 3 ： 5$ ，则 $B F ： C F$ 等于（）

A、5：8 B、3：8 C、3：5 D、2：5

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论错误的是（）

A、 $a > 0$ B、 $a b c > 0$ C、 $b^{2} - 4 a c > 0$ D、 $a + b + c < 0$

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 如图，点P在反比例函数 $y = \frac{k}{x}$ 的图象上，PA⊥x轴于点A ， PB⊥y轴于点B ，且△APB的面积为2，则k等于．

查看试题解析
12. 不透明袋中装有 $3$ 个红球和 $5$ 个绿球，这些球除颜色外无其他差别．从袋中随机摸出 $1$ 个球是红球的概率为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ，过点 $A$ 作 $A M ⊥ B C$ 于点 $M$ ，交 $D E$ 于点 $N$ ．若 $S_{△ A D E} ： S_{△ A B C} = 4 ： 9$ ，则 $A N ： N M =$ ．

查看试题解析
14. 参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有 $x$ 人参加活动，可列方程为

查看试题解析
15. 圆锥的底面半径为3，母线长为5，该圆锥的侧面积为.

查看试题解析
16. 如图，在△ABC中，∠BAC=130°，将 $△ A B C$ 绕点 $C$ 逆时针旋转得到 $△ D E C$ ，点 $A$ ， $B$ 的对应点分别为 $D$ ， $E$ ，连接 $A D$ .当点 $A$ ， $D$ ， $E$ 在同一条直线上时，则 $∠ B A D$ 的大小是 $°$ ．

查看试题解析

三、解答题（本大题共9个小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23每小题9分，第24、25每小题10分，共72分）

17. 计算： $| - \sqrt{2} | - 2 s i n 4 5^{∘} + (1 - \sqrt{5})^{0} + \sqrt{2} \times \sqrt{8}$ ．

查看试题解析
18. $△ A B C$ 在平面直角坐标系内的位置如图（每个小正方形的边长为1）；

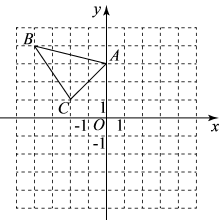(1)、请在这个坐标系内画出 $△ A B C$ 绕原点O顺时针旋转 $90 °$ 得到的的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标；

(2)、请在坐标系内画出 $△ A_{1} B_{1} C_{1}$ 关于原点O对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $C_{2}$ 的坐标；

查看试题解析
19. 如图，一次函数 $y_{1} = - x - 2$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于点 $A (- 1 ， 3)$ 、 $B (n ， - 1)$ ．

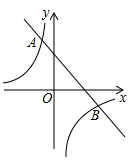(1)、求反比例函数的解析式；

(2)、当 $y_{1} > y_{2}$ 时，直接写出x的取值范围．

查看试题解析
20. 在国家政策的调控下，某市的商品房成交均价由今年3月份的每平方米10000元下降到5月份的每平方米8100元．

(1)、求4、5两月平均每月降价的百分率；

(2)、如果房价继续回落，按此降价的百分率，请你预测到6月份该市的商品房成交均价是否会跌破每平方米7200元？请说明理由．

查看试题解析
21. 为了解中考体育科目的训练情况，长沙市从全市九年级学生中随机抽取了部分学生进行了一次中考体育科目测试，把测试结果分为四个等级：A级优秀、B级良好，C级及格、D级不及格，并将测试结果汇成了如下两幅不完整的统计图，请根据统计图中的信息解答下列问题，

(1)、本次抽样测试的学生人数是；

(2)、扇形统计图中的 $∠ α$ 度数是 $^{∘}$ ，并把图2中的条形图补充完整；

(3)、若全长沙市九年级有学生60000人，如果全部参加这次中考体育测试项目，请估计不及格人数为；

(4)、测试老师想从四位同学（分别记为E、F、G、H ，其中E为小明）随机选取两位同学了解平时的训练情况，请用列表和画树状图的方法求出选中小明的概率．

查看试题解析
22. $2022$ 年 $11$ 月 $9$ 日是我国第 $31$ 个“全国消防宣传日”，该年“ $119$ 消防宣传月”活动的主题是“落实消防责任，防范安全风险”．为落实该主题，济南市消防大队到建东小区进行消防演习．已知，图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂 $A C$ 可伸缩（ $15 m \leq A C \leq 26 m$ ），且起重臂 $A C$ 可绕点A在一定范围内转动，张角为 $∠ C A E$ （ $90 ° \leq ∠ C A E \geq 150 °$ ），转动点A距离地面 $B D$ 的高度 $A E$ 为 $3 m$ ．

(1)、当起重臂 $A C$ 长度为 $20 m$ ，张角 $∠ C A E = 127 °$ ，求云梯消防车最高点C距离地面 $B D$
的高度 $C F$ ；

(2)、已知该小区层高为 $2.8 m$ ，若某居民家突发险情，请问该消防车有效救援能达到几层？请说明理由．（结果精确到 $0.1 m$ ，参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
23. 如图：四边形 $A B C D$ 内接于圆 $O$ ， $∠ B A D = 90 °$ ，对角线 $A C$ 、 $B D$ 交于 $H$ ，点 $E$ 在 $B C$ 的延长线上，且 $∠ C E D = ∠ B A C$ ．

(1)、判断 $D E$ 与圆 $O$ 的位置关系，并说明理由；

(2)、若 $D E ∥ A C$ ，求证： $D$ 为弧 $A C$ 的中点；

(3)、在（2）的条件下，若 $D C = 2$ ， $A B = 2 \sqrt{3}$ ，求劣弧 $A C$ 的长度．

查看试题解析
24. 在 $y$ 关于 $x$ 的函数中，对于实数 $m 、 n (m < n)$ ，当 $m \leq x \leq n$ 时，函数 $y$ 的最大值与最小值之差为 $t$ ，且 $t = 3 (n - m)$ 则称此函数为“倍增函数”；

(1)、当 $m = 1$ ， $n = 3$ 时，判断下列函数是否是“倍增函数”？如果是，请在对应的括号里打“√”，若果不是，请在对应的括号里打“×”
① $y = 3 x$ （ ▲ ），② $y = \frac{9}{x}$ （ ▲ ），③ $y = \frac{1}{2} x^{2} + x - 2$ （ ▲ ）

(2)、当 $m = n - 1 > 0$ 时，反比例函数 $y = \frac{2 m + 5}{x}$ 为“倍增函数”，求 $m$ 的值；

(3)、已知二次函数 $y = x^{2} - n x + m^{2} + 2 m + 1 (m > 0)$ 是“倍增函数”，且 $y$ 的最大值为4，求 $m$ 、 $n$ 的值．

查看试题解析
25. 已知在以点 $B$ 为原点、 $B D$ 所在直线为 $x$ 轴的平面直角坐标系中，圆内接四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于 $E$ ， $A C$ 经过 $△ A B D$ 的内心，且抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过 $B$ 、 $C$ 、 $D$ 三点．

(1)、求证： $A E \cdot E C = B E \cdot D E$ ；

(2)、求证： $A C^{2} = A B \cdot A D + C D^{2}$ ；

(3)、 $△ A B E$ 、 $△ D E C$ 、四边形 $A B C D$ 的面积分别记为 $S_{1}$ ， $S_{2}$ 、S ，求同时满足以下三个条件的抛物线的解析式；
① $\sqrt{S} = \sqrt{S_{1}} + \sqrt{S_{2}}$ ，
② $\sqrt{A C + B D} = \sqrt{B E} + \sqrt{D E}$ ，
③四边形 $A B C D$ 的周长为 $20 \sqrt{2}$ .

查看试题解析