湖南省衡阳市重点中学2023-2024学年七年级上学期月考数学试题
试卷更新日期:2024-01-19 类型:月考试卷
一、选择题
-
1. 的倒数是( )A、 B、7 C、 D、2. 过度包装即浪费又污染环境,据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列结论:①0的相反数、平方、倒数都是它本身;②的系数是;③互补且相等的两个角都是;④等角的余角相等;⑤一个锐角的补角和余角都比这个角大;⑥木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两个点弹出一条墨线,可以用基本事实“两点确定一条直线”来解释.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个5. 下图中不是正方体展开图的是( )A、
 B、
B、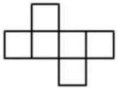 C、
C、 D、
D、 6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定相等的是( )A、
6. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定相等的是( )A、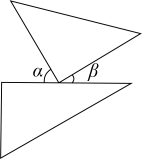 B、
B、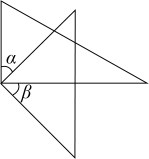 C、
C、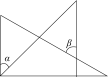 D、
D、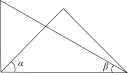 7. 如图, , , , 则与之比为( )
7. 如图, , , , 则与之比为( ) A、 B、 C、 D、8. 三个边长分别为、、的正方形如图摆放,则阴影部分的周长( )
A、 B、 C、 D、8. 三个边长分别为、、的正方形如图摆放,则阴影部分的周长( ) A、只与 , 有关 B、只与、有关 C、只与、有关 D、与 , 、有关9. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( )
A、只与 , 有关 B、只与、有关 C、只与、有关 D、与 , 、有关9. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( ) A、 B、 C、 D、10. “科赫曲线”是瑞典数学家科赫构造的图案(又名雪花曲线).其过程是:第一次操作,将一个等边三角形每边三等分,再以中间一段为边向外作等边三角形,然后去掉中间一段,得到边数为12的图②.第二次操作,将图②中的每条线段三等分,重复上面的操作,得到边数为48的图③.如此循环下去,得到一个周长无限的“雪花曲线”.则操作4次后所得“雪花曲线”的边数是( )
A、 B、 C、 D、10. “科赫曲线”是瑞典数学家科赫构造的图案(又名雪花曲线).其过程是:第一次操作,将一个等边三角形每边三等分,再以中间一段为边向外作等边三角形,然后去掉中间一段,得到边数为12的图②.第二次操作,将图②中的每条线段三等分,重复上面的操作,得到边数为48的图③.如此循环下去,得到一个周长无限的“雪花曲线”.则操作4次后所得“雪花曲线”的边数是( )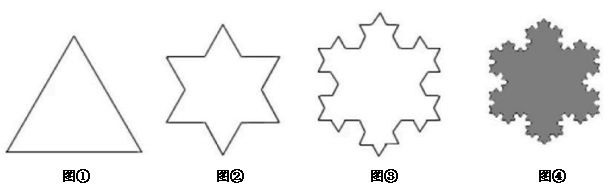 A、192 B、243 C、256 D、768
A、192 B、243 C、256 D、768二、填空题
-
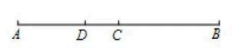
11. 已知 , 则代数式的值是 .12. .13. 如果一个角等于它的余角的2倍,那么这个角的补角是度.14. 如图,线段的长是12,点是线段的中点,点为线段上一点,且 . 线段的长为 .
 15. 如图所示,已知 , , 、分别平分、 . 则的度数为(用含有、的式子表示).
15. 如图所示,已知 , , 、分别平分、 . 则的度数为(用含有、的式子表示). 16. 如图所示, , 、、分别平分 , , , 下列结论:① . ② . ③ . ④ . 其中正确的是 .
16. 如图所示, , 、、分别平分 , , , 下列结论:① . ② . ③ . ④ . 其中正确的是 .
三、解答题
-
17. 计算:(1)、;(2)、 .18. 先化简,再求值: , 其中 , 满足 .19.(1)、若 , 互为相反数, , 互为倒数,是最大的负整数, , 在数轴上对应的两点的距离是5且在的右边,求的值.(2)、有理数 , , 位置如图所示,化简 .
 20. 延长线段至 , 点、分别是线段和线段的中点.
20. 延长线段至 , 点、分别是线段和线段的中点. (1)、已知 , , 求的长;(2)、若 , 求线段的长.21. 滴滴快车是一种便捷的出行工具,计价规则如下表:
(1)、已知 , , 求的长;(2)、若 , 求线段的长.21. 滴滴快车是一种便捷的出行工具,计价规则如下表:计费项目
里程费
时长费
远途费
单价
元/公里
元/分钟
元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算:时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收元.
(1)、若小东乘坐滴滴快车,行车里程为15公里,行车时间为20分钟,则需付车费多少元?(2)、若小明乘坐滴滴快车,行车里程为公里,行车时间为分钟,则小明应付车费多少元(用含、的代数式表示,并化简)?(3)、小王与小张各自乘坐滴滴快车,行车里程分别为公里与公里,但下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?22. 如图为直线上一点, , 平分 , . (1)、的余角有(填图中已有的角);(2)、求的度数;(3)、试判断是否平分 , 并说明理由.23. 探索规律.
(1)、的余角有(填图中已有的角);(2)、求的度数;(3)、试判断是否平分 , 并说明理由.23. 探索规律. (1)、观察上面的图,发现:
(1)、观察上面的图,发现:图①空白部分小正方形的个数是;
图②空白部分小正方形的个数是;
图③空白部分小正方形的个数是 .
(2)、像这样继续排列下去,你会发现一些有趣的规律, .(3)、运用规律计算:24. 若、、三点共线, , 将一个三角板的直角顶点放在点处(注: , ). (1)、如图1,使三角板的长直角边在射线上,则;(2)、将图1中的三角板绕点以每秒的速度按逆时针方向旋转一周,
(1)、如图1,使三角板的长直角边在射线上,则;(2)、将图1中的三角板绕点以每秒的速度按逆时针方向旋转一周,①若旋转到到图2位置,此时 , 求运动时间的值:
②经过秒后,直线恰好成为的三等分线,直接写出的值.
25. 在长方形 中,边 长度比 长度短10个单位长度,且 的长度是 长度的 .(1)、求 边的长;(2)、现有一动点 从 点出发,以每秒2个单位长度的速度沿折线路径 向终点 运动,在 点运动过程中,设运动时间为 秒,三角形 的面积为 ,试用含 的式子表示 ;(3)、在(2)的条件下,点 为 的中点,点 为 的中点,在点 出发的同时,动点 从点 出发,以4个单位/秒的速度沿 边匀速向左运动,当点 遇到点 后,立即按原速原路返回(调头时间忽略不计),且 回到点 时 、 两点立即停止运动.当 时,请求出满足条件的 值?