江西省南昌市师大附中2023-2024学年七年级上学期月考数学试题
试卷更新日期:2024-01-19 类型:月考试卷
一、选择题(每小题3分,共计24分)
-
1. 下列图形属于棱锥的是( )A、
 B、
B、 C、
C、 D、
D、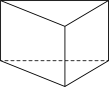 2. 下列运用等式的性质对等式进行的变形中,错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )A、
2. 下列运用等式的性质对等式进行的变形中,错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )A、 B、
B、 C、
C、 D、
D、 4. 下列说法正确的是( )A、的常数项是1 B、0不是单项式 C、的次数是3 D、的系数是 , 次数是35. 下列哪个图形是正方体的展开图( )A、
4. 下列说法正确的是( )A、的常数项是1 B、0不是单项式 C、的次数是3 D、的系数是 , 次数是35. 下列哪个图形是正方体的展开图( )A、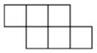 B、
B、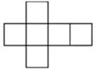 C、
C、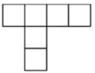 D、
D、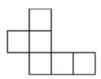 6. 如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩然后拉一条直的参照线,其运用到的数学原理是( )
6. 如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩然后拉一条直的参照线,其运用到的数学原理是( ) A、经过一点有无数条直线 B、经过两点,有且仅有一条直线 C、两点之间,线段最短 D、以上都不对7. 将如图中的图形绕虚线旋转一周,形成的几何体是( )
A、经过一点有无数条直线 B、经过两点,有且仅有一条直线 C、两点之间,线段最短 D、以上都不对7. 将如图中的图形绕虚线旋转一周,形成的几何体是( )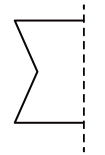 A、
A、 B、
B、 C、
C、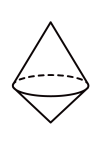 D、
D、 8. 如图,点C、D是线段AB上任意两点,点M是AC的中点,点N是DB的中点,若 , , 则线段CD的长是( )
8. 如图,点C、D是线段AB上任意两点,点M是AC的中点,点N是DB的中点,若 , , 则线段CD的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共计24分)
-
9. 2023年12月4日,财政部、应急管理部下达亿元中央自然灾害救灾资金,切实解决受灾群众生活困难,确保安全温暖过冬.将数据亿用科学记数法表示应为 .10. 若代数式的值与互为相反数,则 .11. 若已知与是同类项,则 .12. 已知关于x的方程是一元一次方程,则 .13. 已知当时,代数式的值为2023;则当时,代数式的值为 .14. 如图,是一段高铁行驶路线图,图中字母表示的5个点表示5个车站,在这段路线上往返行车,需印制种车票.
 15. 七年级一位同学用围棋棋子按照某种规律摆出“师大附中”中的“大”字,如图①,图②,图③,.….,按照这种规律,第n个“大”字中的棋子个数是 .
15. 七年级一位同学用围棋棋子按照某种规律摆出“师大附中”中的“大”字,如图①,图②,图③,.….,按照这种规律,第n个“大”字中的棋子个数是 .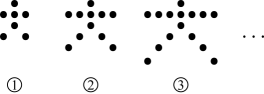 16. 关于x的方程有整数解,则正整数a所有可能取值为 .
16. 关于x的方程有整数解,则正整数a所有可能取值为 .三、解答题(17-20每题6分,21、22每题8分,23题12分,共52分)
-
17.(1)、计算:;(2)、解方程: .18. 如图,已知平面上四个点A , B , C , D , 请按要求完成下列问题:
 (1)、画直线 , 射线 , 连接;(2)、在线段上求作点P , 使得;(保留作图痕迹)19. A、B、C、D四个站的位置如图所示.
(1)、画直线 , 射线 , 连接;(2)、在线段上求作点P , 使得;(保留作图痕迹)19. A、B、C、D四个站的位置如图所示. (1)、分别表示出A、D两站之间的距离和A、C两站之间的距离;(2)、若 , C为的中点,求b的值.20. 某工厂需要生产一批太空漫步器(如图),每套设备由一个支架和两套脚踏板组装而成;工厂现共有45名工人,每人每天平均生产60个支架或96套脚踏板.
(1)、分别表示出A、D两站之间的距离和A、C两站之间的距离;(2)、若 , C为的中点,求b的值.20. 某工厂需要生产一批太空漫步器(如图),每套设备由一个支架和两套脚踏板组装而成;工厂现共有45名工人,每人每天平均生产60个支架或96套脚踏板. (1)、应如何分配工人才能使每天生产的支架和脚踏板恰好配套?(2)、若每套太空漫步器的成本为240元,要达到的利润率,则每套应定价多少元?21. 如图,已知点C为上一点, , , D , E分别为 , 的中点,
(1)、应如何分配工人才能使每天生产的支架和脚踏板恰好配套?(2)、若每套太空漫步器的成本为240元,要达到的利润率,则每套应定价多少元?21. 如图,已知点C为上一点, , , D , E分别为 , 的中点,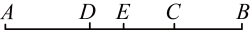 (1)、求的长;(2)、求的长.22. 聪聪根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
(1)、求的长;(2)、求的长.22. 聪聪根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图: (1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;
(1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;用户
张大爷
刘奶奶
王阿姨
聪聪家
用户
输入()
8
15
18
25
输入()
输出(元)
24
a
60
b
输出(元)
(3)、小丽家比小明家用水量多 , 水费多44元,则小丽家该月用水多少?23. 已知:点A、B、P为数轴上三点,我们规定:点P到点A的距离是点P到点B的距离的k倍,则称P是的“k倍点”,记作: , 例如:若点P表示的数为0,点A表示的数为 , 点B表示的数为1,则P是的“2倍点”,记作: .
 (1)、如图,A、B、P为数轴上三点,回答下面问题:
(1)、如图,A、B、P为数轴上三点,回答下面问题:① ▲ ;
②若点C在数轴上且 , 则点C表示的数为 ▲ ;
③若点D是数轴上一点,且 , 求点D所表示的数.
(2)、数轴上,点E表示的数为 , 点F表示的数为50,点M、N为线段上的两点,且 , , 求的长度.