山东省聊城市多校联考2023-2024学年八年级上学期12月月考数学试题

试卷更新日期：2024-01-19 类型：月考试卷

进入出卷网下载

一、选择题（共12小题，每小题3分，在每小题给出的四个选项中，只有一项符合题目要求）

1. 下列手机中的图标是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，已知 $∠ 1 = ∠ 2 ， A C = A D$ ，增加下列条件：不能使 $△ A B C ≌ △ A E D$ 的条件（）

A、 $B C = E D$ B、 $A B = A E$ C、 $∠ C = ∠ D$ D、 $∠ B = ∠ E$

查看试题解析
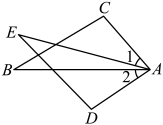3. 等腰三角形的一个内角为50°，则另外两个角的度数分别为（）

A、65°，65° B、50°，80° C、65°，65°或50°，80° D、50°，50°

查看试题解析
4. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在 $△ A B C$ （）

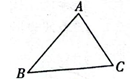A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处

查看试题解析
5. 若点 $A (a ， - 1)$ 与点 $B (2 ， b)$ 关于y轴对称，则 $a - b$ 的值是（）

A、 $- 1$ B、 $- 3$ C、1 D、2

查看试题解析
6. 当分式 $\frac{x + 3}{x^{2} - 4}$ 的值为0时，x的值为（）

A、2 B、 $- 3$ C、 $- 2$ D、 $\pm 2$

查看试题解析
7. 一名警察在高速公路上随机观察了6辆汽车的车速，记录如下：
车序号
1
2
3
4
5
6
车速（千米/时）
100
82
90
82
70
84
则这6辆车车速的众数和中位数是（）

A、84，90 B、85，82 C、82，86 D、82，83

查看试题解析
8. 下列各式从左到右的变形正确的是（）

A、 $\frac{b}{a - b} = \frac{- b}{a + b}$ B、 $\frac{0.2 a + b}{a + 0.2 b} = \frac{2 a + b}{a + 2 b}$ C、 $- \frac{x + 1}{x - y} = \frac{x - 1}{x - y}$ D、 $\frac{x - \frac{1}{2} y}{\frac{1}{2} x + y} = \frac{2 x - y}{x + 2 y}$

查看试题解析
9. 将分式 $\frac{x^{2}}{x + y}$ 中的x、y的值同时扩大2倍，则分式的值（）

A、扩大2倍 B、缩小到原来的 $\frac{1}{2}$ C、保持不变 D、无法确定

查看试题解析
10. 如图，把 $△ A B C$ 沿线段 $D E$ 折叠，使点B落在点F处；若 $A C ∥ D E$ ， $∠ A = 70 °$ ， $A B = A C$ ，则 $∠ C E F$ 的度数为（）

A、 $40 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
11. 某列车提速前行驶 $400 k m$ 与提速后行驶 $500 k m$ 所用时间相同，若列车平均提速 $20 k m / h$ ，设提速后平均速度为 $x k m / h$ ，所列方程正确的是（）

A、 $\frac{400}{x} = \frac{500}{x + 20}$ B、 $\frac{400}{x} = \frac{500}{x - 20}$ C、 $\frac{400}{x - 20} = \frac{500}{x}$ D、 $\frac{400}{x + 20} = \frac{500}{x}$

查看试题解析
12. 如图，在Rt△ABC中，∠ACB＝90°，∠CAB＝36°，以C为原点，AC所在直线为y轴，BC所在直线为x轴建立平面直角坐标系，在坐标轴上取一点M使△MAB为等腰三角形，符合条件的M点有（）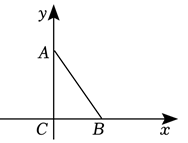

A、5个 B、6个 C、7个 D、8个

查看试题解析

二、填空题（共5小题，共15分）

13. 若 $\frac{y}{x} = \frac{2}{7}$ ，则 $\frac{x - y}{x} =$ ．

查看试题解析
14. 如图，DE是△ABC中AC边的垂直平分线，若BC＝8cm，AB＝10cm，则△EBC的周长为cm．

查看试题解析
15. 某中学八年级某个同学一个学期得平时作业成绩为90分，期中考试成绩为85分，期末考试成绩为88分，如果学校按2：3：5的比例计算总平均分，那么这个同学的总平均分为分．

查看试题解析
16. 关于x的方程 $\frac{x}{x - 3}$ +1= $\frac{m}{x - 3}$ 有增根，则m的值为．

查看试题解析
17. 如图，已知：∠MON=30°，点A₁、A₂、A₃ 在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，若OA₁=a，则△A₆B₆A₇的边长为．

查看试题解析

三、解答题（共8小题，共69分）

18. 解方程：

(1)、 $\frac{1}{x - 1} = \frac{5}{2 x + 1}$ ；

(2)、 $\frac{16}{x^{2} - 4} + 1 = \frac{2 + x}{x - 2}$ ．

查看试题解析
19. 化简式子（ $\frac{a^{2} - 2 a}{a^{2} - 4 a + 4} +$ 1） $\div \frac{a^{2} - 1}{a^{2} + a}$ ，并在﹣2，﹣1，0，1，2中选取一个合适的数作为a的值代入求值.

查看试题解析
20. 如图， $A C / / D F ， A D = B E ， B C / / E F$ ．求证： $△ A B C ≌ △ D E F$ ．

查看试题解析
21. $△ A B C$ 在平面直角坐标系中的位置如图所示．

(1)、请直接写出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ 三个顶点的坐标（其中 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 分别是A ， B ， C的对应点）；

(2)、请直接写出 $△ A_{1} B_{1} C_{1}$ 关于y轴对称的 $△ A_{2} B_{2} C_{2}$ 三个顶点的坐标（其中 $A_{2}$ ， $B_{2}$ ， $C_{2}$ 分别是A ， B ， C的对应点）；

(3)、在直线l上找到一点P ，使得 $P A + P B$ 最小．

查看试题解析
22. 某学校从九年级同学中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试，根据测试成绩绘制出统计表和如图所示的统计图（成绩均为整数，满分为10分）．
甲组成绩统计表：
成绩
7
8
9
10
人数
1
9
5
5
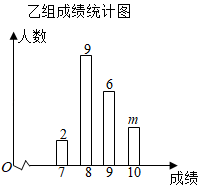
根据上面的信息，解答下列问题：

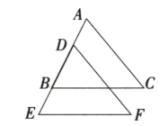
(1)、甲组的平均成绩为分， $m =$ ，甲组成绩的中位数是分，乙组成绩的众数是分；

(2)、若已经计算出甲组成绩方差为0.81，求出乙组成绩的方差，并判断哪个小组的成绩更加稳定？

查看试题解析
23. 如图， $A D$ 平分 $∠ B A C$ 交 $B C$ 于 $D$ ， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别为 $E$ 、 $F$ ．求证： $A D$ 垂直平分 $E F$ ．

查看试题解析
24. 为顺利通过“文明城市”验收，我市拟对城区部分排水骨干道公用设施全面更新改造，为响应城市建设的需要，需在一个月内完成工程，现有甲、乙两个工程队有意承包这项工程，经调查知道，乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的1.5倍，若甲、乙两工程队合作只需12天完成．

(1)、甲、乙两个工程队单独完成此项工程各需多少天？

(2)、若甲工程队每天的工程费用是4万元，乙工程队每天的工程费用是3万元，请你设计一种方案，既能按时完工，又能使工程费用最少．

查看试题解析
25. 如图1，已知在等边 $△ A B C$ 中，当点D在 $B C$ 边上，点E在 $A C$ 边上，且 $B D = C E$ ，连接 $A D 、 B E$ ，交于点F ．（等边三角形3条边相等，每个角都是 $60 °$ ）

(1)、求证： $∠ A F E = ∠ A B D$ ；

(2)、如图2，当点D在 $B C$ 的延长线上，点E在 $C A$ 的延长线上，而其它条件不变时， $∠ A F E$ 与 $∠ A B D$ 又有怎样的数量关系？请说明理由；

(3)、如图3，当点D在 $C B$ 的延长线上，点E在 $A C$ 的延长线上，而其它条件不变时， $∠ A F E$ 与 $∠ A B D$ 又有怎样的数量关系？请直接写出关系，不必证明．

查看试题解析

车序号	1	2	3	4	5	6
车速（千米/时）	100	82	90	82	70	84

成绩	7	8	9	10
人数	1	9	5	5