山东省济宁市嘉祥县2023-2024学年八年级上学期12月月考数学试题
试卷更新日期:2024-01-19 类型:月考试卷
一、单选题
-
1. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代 表“大雪”、“白露”、“芒种”、“立春”,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,能组成三角形的是( )A、1,6,7 B、2,5,8 C、3,4,5 D、5,5,103. 下列计算正确的是( )A、 B、 C、 D、4. 如图,已知点、、、在同一条直线上, , , 添加一个条件仍无法证明是( )
2. 下列长度的三条线段,能组成三角形的是( )A、1,6,7 B、2,5,8 C、3,4,5 D、5,5,103. 下列计算正确的是( )A、 B、 C、 D、4. 如图,已知点、、、在同一条直线上, , , 添加一个条件仍无法证明是( ) A、 B、 C、 D、5. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
A、 B、 C、 D、5. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )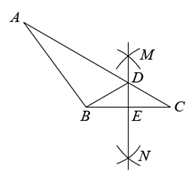 A、25 B、22 C、19 D、186. 如图,在中,知点 , , 分别为 , , 的中点, , 则阴影部分的面积( )
A、25 B、22 C、19 D、186. 如图,在中,知点 , , 分别为 , , 的中点, , 则阴影部分的面积( )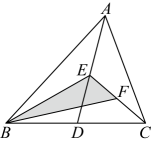 A、4 B、2 C、1 D、7. 已知 ,则 ( )A、1 B、6 C、7 D、128. 如图1,在边长为的正方形中剪去一个边长为的小正方形 , 把剩下部分拼成一个梯形(如图 , 利用这两幅图形面积,可以验证的公式是( )
A、4 B、2 C、1 D、7. 已知 ,则 ( )A、1 B、6 C、7 D、128. 如图1,在边长为的正方形中剪去一个边长为的小正方形 , 把剩下部分拼成一个梯形(如图 , 利用这两幅图形面积,可以验证的公式是( )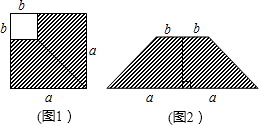 A、 B、 C、 D、9. 已知:如图,在长方形中, . 延长到点E , 使 , 连接 , 动点P从点B出发,以每秒2个单位的速度沿向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,和全等.
A、 B、 C、 D、9. 已知:如图,在长方形中, . 延长到点E , 使 , 连接 , 动点P从点B出发,以每秒2个单位的速度沿向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,和全等.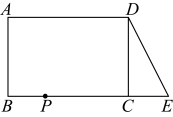 A、1 B、1或3 C、1或7 D、3或710. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作等边△ABC和等边△ECD , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q连接PQ . 以下五个结论正确的是( )
A、1 B、1或3 C、1或7 D、3或710. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作等边△ABC和等边△ECD , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q连接PQ . 以下五个结论正确的是( )① ;②PQ∥AE; ③ ;④ ;⑤
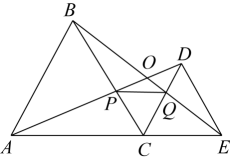 A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤
A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤二、填空题
-
11. 在平面直角坐标系中,已知与点关于轴对称的点的坐标为 .12. 分解因式: .13. 已知是完全平方式,则.14. 如图,已知△ABC的两边AB=5,AC=8,BO、CO分别平分∠ABC、∠ACB,过点O作DE∥BC,则△ADE的周长等于 .
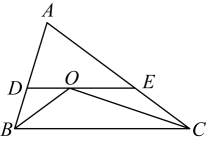 15. 如图,∠MON=90°,点A , B分别在射线OM , ON上运动,BE平分∠NBA , BE的反向延长线与∠BAO的平分线交于点C , 则∠C=°.
15. 如图,∠MON=90°,点A , B分别在射线OM , ON上运动,BE平分∠NBA , BE的反向延长线与∠BAO的平分线交于点C , 则∠C=°.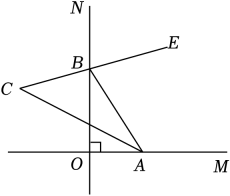 16. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .
16. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .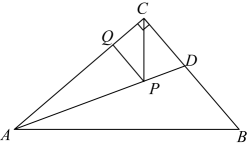
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,在中,点在边上.
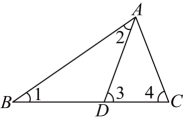 (1)、若 , 求的度数;(2)、若为的中线,的周长比的周长大 , 求的长.19. 如图,公园里有一条“Z”字形道路 , 在三段路旁各有一只小石凳 , 且恰好在一条直线上,为的中点.
(1)、若 , 求的度数;(2)、若为的中线,的周长比的周长大 , 求的长.19. 如图,公园里有一条“Z”字形道路 , 在三段路旁各有一只小石凳 , 且恰好在一条直线上,为的中点.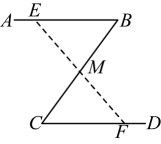 (1)、求证;(2)、判断与的位置关系,并说明理由.20. 如图,在中, , , 平分交AD于点D .
(1)、求证;(2)、判断与的位置关系,并说明理由.20. 如图,在中, , , 平分交AD于点D .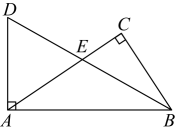 (1)、求证:;(2)、若 , , 求的面积.21. 如图,三个顶点的坐标分别为 , , .
(1)、求证:;(2)、若 , , 求的面积.21. 如图,三个顶点的坐标分别为 , , . (1)、画出关于x轴对称的图形 , 并写出三个顶点的坐标;(2)、求的面积(3)、在x轴上作出一点P , 使的值最小.(保留作图痕迹)22. 如图所示,小红在一块长为米,宽为米的长方形空地上进行绿化改造,若在中间修建一边长为米的正方形花坛,其余地面铺设草坪(阴影部分)
(1)、画出关于x轴对称的图形 , 并写出三个顶点的坐标;(2)、求的面积(3)、在x轴上作出一点P , 使的值最小.(保留作图痕迹)22. 如图所示,小红在一块长为米,宽为米的长方形空地上进行绿化改造,若在中间修建一边长为米的正方形花坛,其余地面铺设草坪(阴影部分) (1)、用含a , b的式子表示草坪的总面积:(2)、当时,已知草坪的单价为每平方米元.求需要购买草坪所需要的总费用.23. 如图,于于F,若 ,
(1)、用含a , b的式子表示草坪的总面积:(2)、当时,已知草坪的单价为每平方米元.求需要购买草坪所需要的总费用.23. 如图,于于F,若 ,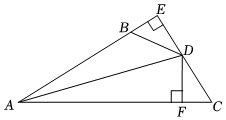 (1)、求证:平分;(2)、已知 , 求的长.24. 乘法公式的探究及应用.
(1)、求证:平分;(2)、已知 , 求的长.24. 乘法公式的探究及应用.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
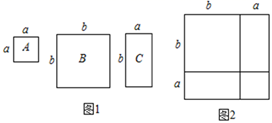 (1)、观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系.;(2)、若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张, C号卡片张.(3)、根据(1)题中的等量关系,解决问题:已知:a+b=5,a2+b2=11,求ab的值.25. 先阅读下面的材料,再分解因式.
(1)、观察图2,请你写出下列三个代数式:(a+b)2 , a2+b2 , ab之间的等量关系.;(2)、若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张, C号卡片张.(3)、根据(1)题中的等量关系,解决问题:已知:a+b=5,a2+b2=11,求ab的值.25. 先阅读下面的材料,再分解因式.要把多项式分解因式,可以先把它的前两项分成一组,并提出a , 再把它的后两项分成一组,并提出b , 从而得 .
这时,由于中又有公因式 , 于是可提公因式 , 从而得到 , 因此有 .
这种因式分解的方法叫做“分组分解法”,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来分解因式.
(1)、请用上面材料中提供的方法分解因式:①;
②;
③ .
(2)、已知的三边长为 , , , 并且 , 试判断此三角形的形状.26.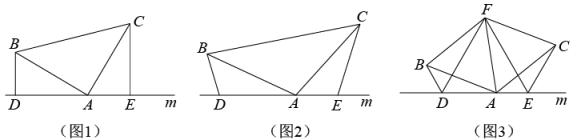 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC , 直线m经过点A , BD⊥直线m , CE⊥直线m , 垂足分别为点D、E . 证明∶DE=BD+CE .(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE , 若∠BDA=∠AEC=∠BAC , 试判断△DEF的形状.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC , 直线m经过点A , BD⊥直线m , CE⊥直线m , 垂足分别为点D、E . 证明∶DE=BD+CE .(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC , D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE , 若∠BDA=∠AEC=∠BAC , 试判断△DEF的形状.