吉林省白山市靖宇县2023-2024学年八年级上学期数学期末考试试卷

试卷更新日期：2024-01-19 类型：期末考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在下列长度的三条线段中，能围成三角形的是（）

A、2，3，4 B、2，3，5 C、3，5，9 D、8，4，4

查看试题解析
3. 下列计算正确的是（　　）

A、 $a^{4} · a^{3} = a^{12}$ B、 $a^{8} \div a^{4} = a^{2}$ C、 $a^{3} + a^{3} = 2 a^{6}$ D、 ${(a^{2})}^{4} = a^{8}$

查看试题解析
4. 三角形的两条边长为3和7，那么第三边长可能是（）

A、1 B、4 C、7 D、10

查看试题解析
5. 如图，AB∥CD，点E在线段BC上，CD=CE．若∠ABC=30°，则∠D为（）

A、85° B、75° C、60° D、30°

查看试题解析
6. 图中的小正方形边长都相等，若△MNP≌△MFQ ，则点Q可能是图中的（　　）

A、点A B、点B C、点C D、点D

查看试题解析
7. 将一副三角板按图中方式叠放，则角α等于（）

A、30° B、45° C、60° D、75°

查看试题解析
8. 为响应承办“绿色奥运”的号召，九年级（1）班全体师生义务植树300棵．原计划每小时植树x棵，但由于参加植树的全体师生植树的积极性高涨，实际工作效率提高为原计划的1.2倍，结果提前20分钟完成任务．则下面所列方程中，正确的是（）

A、 $\frac{300}{x} - \frac{20}{60} = \frac{300}{1.2 x}$ B、 $\frac{300}{x} - \frac{300}{1.2 x} = 20$ C、 $\frac{300}{x} - \frac{300}{x + 1.2 x} = \frac{20}{60}$ D、 $\frac{300}{x} = \frac{300}{1.2 x} - \frac{20}{60}$

查看试题解析
9. 如图，是由9个等边三角形拼成的六边形，若已知中间最小的三角形的边长是3，则六边形的周长为（　　）

A、90 B、60 C、50 D、30

查看试题解析
10. 如图，七边形ABCDEFG中，AB、ED的延长线交于点O，若∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析

二、填空题（本大题共5个小题，每小题3分，共15分）

11. 已知点P的坐标为（﹣2，3）．则它关于y轴对称的点P'的坐标是．

查看试题解析
12. 计算： $\sqrt{\frac{- 12}{- 3}}$ = ．

查看试题解析
13. （3a²﹣6ab）÷3a= ．

查看试题解析
14. 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4= ．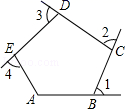

查看试题解析
15. 式子 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ 称为二阶行列式，规定它的运算法则为 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} | = a d - b c$ ，则二阶行列式 $| \begin{array}{l} a^{2} - a \\ a \end{array} \begin{array}{l} 1 \\ \frac{1}{a^{2} - 1} \end{array} | =$ ．

查看试题解析

三、解答题（本大题共8个小题，共75分）

16. 先化简，再求值：已知 $(\frac{x^{2}}{x - 3} + \frac{9}{3 - x}) \div \frac{x - 1}{x^{2} - 2 x + 1}$ ，其中x满足 $x^{2} + 2 x - 5 = 0$ ．

查看试题解析
17. 在△ABC中，AD是△ABC的高，∠B=30°，∠C=52°

(1)、尺规作图：作△ABC的角平分线AE；

(2)、求∠DAE的大小。

查看试题解析
18. 在平面直角坐标系中， $△ A B C$ 的三个顶点的位置如图所示．

(1)、请画出 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ；（其中 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 分别是A ， B ， C的对应点，不写画法）

(2)、直接写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 三点的坐标： $A^{'}$ （）， $B^{'}$ （）， $C^{'}$ （）；

(3)、求 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析
19. 受疫情影响，“84”消毒液需求量猛增，某商场用8000元购进一批“84”消毒液后，供不应求，商场用17600元购进第二批这种“84”消毒液，所购数量是第一批数量的2倍，但单价贵了1元

(1)、求该商场购进的第一批“84”消毒液的单价；

(2)、商场销售这种“84”消毒液时，每瓶定价为13元，最后200瓶按9折销售，很快售完，在这两笔生意中商场共获利多少元？

查看试题解析
20. 如图，在△ABC中，∠B＝60°，点M从点B出发沿线段BC方向，在线段BC上运动．在点M运动的过程中，连结AM，并以AM为边在线段BC上方，作等边△AMN，连结CN．

(1)、当∠BAM＝°时，AB＝2BM；

(2)、请添加一个条件：，使得△ABC为等边三角形；当△ABC为等边三角形时，求证：CN+CM＝AC．

查看试题解析
21. 阅读材料：把形 $a x^{2} + b x + c$ 的二次三项式（或其一部分）配成完全平方式的方法叫配方法．配方法的基本形式是完全平方公式的逆写，即 $a^{2} \pm 2 a b + b^{2} = {(a \pm b)}^{2}$ ．请根据阅读材料解决下列问题：

(1)、填空： $a^{2} - 4 a + 4 =$ ．

(2)、先化简，再求值： $(a + b) (a - b) + (2 a^{3} b - 4 a b^{3}) \div 2 a b$ ，其中 $a 、 b$ 满足 $a^{2} + 2 a + b^{2} - 6 b + 10 = 0$ ．

(3)、若 $a 、 b 、 c$ 分别是 $Δ A B C$ 的三边，且 $a^{2} + 4 b^{2} + c^{2} - 2 a b - 6 b - 2 c + 4 = 0$ ，试判断 $Δ A B C$ 的形状，并说明理由．

查看试题解析
22. 如图， $∠ B A D = ∠ C A E = 90 °$ ， $A B = A D$ ， $A E = A C$ ， $A F ⊥ C F$ ，垂足为 F ．

(1)、求证： $△ A B C ≌ △ A D E$ ；

(2)、若 $A C = 10$ ，求四边形 $A B C D$ 的面积；

(3)、求 $∠ F A E$ 的度数．

查看试题解析
23. 通过对下面数学模型的研究学习，解决下列问题：

(1)、【模型呈现】
如图1， $∠ B A D ＝ 90 ° ， A B ＝ A D$ ，过点B作 $B C ⊥ A C$ 于点C，过点D作 $D E ⊥ A C$ 于点E．由 $∠ 1 + ∠ 2 = ∠ 2 + ∠ D = 90 °$ ，得 $∠ 1 = ∠ D$ ．又 $∠ A C B = ∠ A E D = 90 °$ ，可以推理得到 $△ A B C ≌ △ D A E$ ．进而得到AC＝， BC＝．我们把这个数学模型称为“K字”模型或“一线三等角”模型；

(2)、【模型应用】
①如图2， $∠ B A D = ∠ C A E = 90 ° ， A B ＝ A D ， A C ＝ A E$ ，连接 $B C ， D E$ ，且 $B C ⊥ A F$ 于点F， $D E$ 与直线 $A F$ 交于点G．求证：点G是 $D E$ 的中点；
②如图3，在平面直角坐标系xOy中，点A的坐标为 $(2 ， 4)$ ，点B为平面内任一点．若 $△ A O B$ 是以 $O A$ 为斜边的等腰直角三角形，请直接写出点B的坐标．

查看试题解析