吉林省白山市靖宇县2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-01-19 类型:期末考试
一、选择题:(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 我国民间,流传着许多含有吉祥意义的文字图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”、“禄”、“寿”、“喜”,其中是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程的两根分别为( )A、 B、 C、 , D、 ,3. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、且 C、且 D、且4. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、
2. 一元二次方程的两根分别为( )A、 B、 C、 , D、 ,3. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、且 C、且 D、且4. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、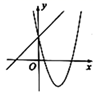 B、
B、 C、
C、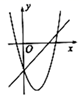 D、
D、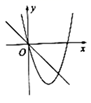 5. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
5. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )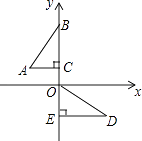 A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移36. 连续四次抛掷一枚硬币都是正面朝上,则第五次抛掷正面朝上的是( )A、必然事件 B、不可能事件 C、随机事件 D、确定事件7. 如图,是△ABC的外接圆, , 则∠A的大小为( )
A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移36. 连续四次抛掷一枚硬币都是正面朝上,则第五次抛掷正面朝上的是( )A、必然事件 B、不可能事件 C、随机事件 D、确定事件7. 如图,是△ABC的外接圆, , 则∠A的大小为( ) A、30° B、60° C、80° D、120°8. 如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( )
A、30° B、60° C、80° D、120°8. 如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( ) A、30° B、40° C、50° D、60°9. 如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
A、30° B、40° C、50° D、60°9. 如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( ) A、3 米 B、5米 C、7米 D、8米10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是( )
A、3 米 B、5米 C、7米 D、8米10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题:(本大题共8个小题,每小题3分,共24分.把答案写在题中横线上)
-
11. 若关于x的方程 是一元二次方程,则m的值是 .12. 已知抛物线经过、、三点,则、、的大小关系是 (用“<”连接)13. 正五边形的中心角的度数是 .14. 将分别标有“学”“习”“强”“国”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“强国”的概率是 .15. 将抛物线向左平移2个单位后,得到的抛物线的解析式是;16. 新冠病毒在无防护下传播速度很快,已知有1个人感染了病毒,经过两轮传染后共有625个人感染了病毒,若每轮传染中平均一个人传染m个人,则可列方程为;17. 在一个不透明的袋子里装有若干个白球和6个黄球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过很多次重复试验,发现摸到黄球的频率稳定在0.75,则袋中白球有个;18. 如图,△ABC,AC=3,BC=4,∠C=90°,⊙O为△ABC的内切圆,与三边的切点分别为D、E、F,则⊙O的面积为(结果保留π)

三、解答题:(第19题5分×2=10分,第20题12分,共22分)
-
19. 用适当的方法解下列一元二次方程(1)、(2)、20. 如图,有一直径是的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC .
 (1)、求AB的长;(2)、用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
(1)、求AB的长;(2)、用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.四、解答题:(第21题12分,第22题12分,共24分)
-
21. 现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和 万件,现假定该公司每月投递的快件总件数的增长率相同.(1)、求该公司投递快件总件数的月平均增长率;(2)、如果平均每人每月可投递快递 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?22. 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为O(0,0)A(5,3),B(0,5).
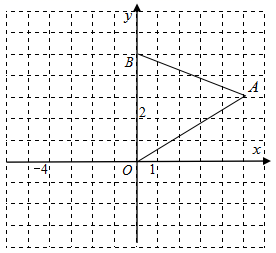 (1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.
(1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.五、解答题:(第23题12分,第24题12分,共24分)
-
23. 为了做好防控H1N1甲型流感工作,我县卫生局准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士指导某乡镇预防H1N1甲型流感工作.(1)、若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果.(2)、求恰好选中医生甲和护士A的概率.24. 2020年是脱贫攻坚的收官司之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于50元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如表所示.
销售单价x(元)
30
40
45
销售数量y(件)
100
80
70
(1)、求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、销售单价定为多少元时,每天的销售利润为800元?(3)、销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少元?六、解答题:(本题满分12分)

