浙江省浙师大省联考2023-2024学年八年级第一学期数学12月月考试卷

试卷更新日期：2024-01-18 类型：月考试卷

进入 出卷网 下载

一、选择题(本大题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)

  • 1. 城市标志可以间接反映一座城市的文化，起到对城市的识别与推广作用.下列我省四个城市标志图案中，是轴对称图形的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 一个不等式的解表示在数轴上如图所示，则这个不等式可以是（ ）

    A、2x≥6 B、x-3<0 C、3-x<0 D、x+3>0

    查看试题解析

  • 3. 下列选项中，能用来说明命题“若a2>1，则a>1”是假命题的反例是（ ）
    A、a=1 B、a=2 C、a=-1 D、a=-2

    查看试题解析

  • 4. 小聪上午8：00从家里出发，骑车去一家文具店购物，然后从这家文具店返回家中.小聪离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示.根据图象，下列结论不正确的是（ ）

    A、文具店距小聪家4千米 B、小聪在文具店逗留了30分钟 C、小聪去文具店途中速度大于回家途中速度 D、小聪在来去途中，离家2千米的时间是8：50

    查看试题解析

  • 5. 如图，已知AB=AD，那么添加下列条件后，仍无法判定△ABC≌△ADC的是（ ）

    A、∠BCA=∠DCA B、∠BAC=∠DAC C、CB=CD D、∠B=∠D=90°

    查看试题解析

  • 6. 如图，D为BC延长线上一点，点E在AB上，连结DE交AC于点F.若DB=DE，∠A=35°，∠D=30°，则∠ACD的度数是（ ）

    A、115° B、110° C、105° D、95°

    查看试题解析

  • 7. 通过如下尺规作图，能确定D是BC边中点的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 8. 如图，在Rt△ABC中，∠A=90°，∠B=30°.动点P从点C出发，沿边CB，BA向点A运动.在点P运动过程中，△PAC可能成为的特殊三角形依次是（ ）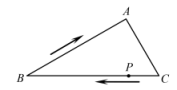

    A、直角三角形→等边三角形→直角三角形→等边三角形→直角三角形 B、等腰三角形→直角三角形→等边三角形→直角三角形→等腰直角三角形 C、直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形 D、等腰直角三角形→等腰三角形→直角三角形→等腰直角三角形→直角三角形

    查看试题解析

  • 9. 如图，四盏相同的灯笼放置在平面直角坐标系中，坐标分别是A(-3.5，b)，B(-2，b)，C(-1，b)，D(1，b)，将其中一盏灯笼向右平移m个单位，使得y轴两侧的灯笼对称，则m的值可以是（ ）

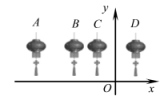    A、3 B、4 C、4.5 D、5.5

    查看试题解析

  • 10. 若x<y，且ax>ay，当x≥-1时，关于x的代数式ax-2恰好能取到两个非负整数值，则a的取值范围是（ ）
    A、-4<a≤-3 B、-4≤a<-3 C、-4<a<0 D、a≤-3

    查看试题解析

二、填空题(本大题有6小题,每小题4分,共24分)

  • 11. 函数y= 1x−5 中，自变量x的取值范围是

    查看试题解析

  • 12. 点A(-1，2)关于x轴的对称点A'的坐标是.

    查看试题解析

  • 13. 国内航空公司规定：旅客乘机时，免费携带行李箱的长，宽，高三者之和不能超过115cm.某厂家生产符合该规定的行李箱.已知行李箱的宽为15cm，长与高的比为2∶3，则符合此规定的行李箱的高的最大值为cm.

    查看试题解析

  • 14. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E，则∠EDC=.

    查看试题解析

  • 15. 小明将两把完全一样的直尺如图放置在∠AOB上，两把直尺的接触点为P，边OA与其中一把直尺边缘的交点为C，点C，P在这把直尺上的刻度读数分别是2和5，则OC的长度是cm.

    查看试题解析

  • 16. 已知，在Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，点D在斜边AB上，将Rt△ABC沿着过点D的一条直线翻折，使点B落在射线BC上的B'处，连结DB'，AB'.
    (1)、当D是AB的中点时，S△AB'D=.
    (2)、当△AB'D是直角三角形时，AD的长是.

    查看试题解析

三、解答题(本大题有8小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤)

  • 17. 如图是某校区域示意图.规定列号写在前面，行号写在后面.

    (1)、用数对的方法表示校门的位置.
    (2)、数对(9，7)在图中表示什么地方?

    查看试题解析

  • 18. 解不等式组{2−3x≤4−x ， ①1−2x−12＞x4.②

    下面是某同学的部分解答过程，请认真阅读并完成任务：

    解：解不等式①，得-3x+x≤4-2.第1步

    合并同类项，得-2x≤2.第2步

    两边都除以-2，得x≤-1.第3步

    任务一：该同学的解答过程中第    ▲    步出现了错误，这一步的依据是    ▲     ， 不等式①的正确解是    ▲    .

    任务二：解不等式②，并写出该不等式组的解集.

    查看试题解析

  • 19. 如图，在平面直角坐标系中，△ABC的顶点都在格点上.将△ABC先向左平移2个单位，再向下平移3个单位，得到△A1B1C1.

    (1)、请在图中画出△A1B1C1.
    (2)、△ABC上有点P(a，b)，平移后对应点P1的坐标为(用含a，b的代数式表示).

    查看试题解析

  • 20. 如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连结BD，CE.

    (1)、求证：△ABD≌△ACE.
    (2)、若∠BCE-∠ABC=15°，求∠ABD的度数.

    查看试题解析

  • 21. 已知一条钢筋长90cm，把它折弯成一个等腰三角形框，其底边长记为x(cm)，腰长记为y(cm).
    (1)、求y关于x的函数表达式和自变量x的取值范围.
    (2)、当x=40时，求函数y的值，并求出此时等腰三角形的面积.

    查看试题解析

  • 22. 某校数学兴趣小组活动，准备将一张Rt△ABC纸片进行作图操作，以此来解决相关问题.

    (1)、如图1，需将Rt△ABC纸片裁剪成面积相等的两个三角形.请你用尺规画出裁剪线，保留作图痕迹.
    (2)、如图2，在Rt△ABC纸片中，∠C=90°，∠B=30°，AB=40，需将这张纸片裁剪成一个长方形，使长方形的面积是Rt△ABC面积的一半.

    ①画出裁剪的长方形(画出一种情况即可)；

    ②求裁剪所得到的长方形的周长.

    查看试题解析

  • 23. 根据以下素材，探索完成任务.

    探究奖项设置和奖品采购的方案

    素材1

    如图，某学校举办“迎亚运庆国庆”知识竞赛，分别设置一等奖、二等奖和三等奖的奖品.已知一盒水笔比一本笔记本的单价多10元，6盒水笔和3本笔记本的总价为150元.

    素材2

    若设置的获奖总人数不变，为提高同学们的参赛积极性，学校计划对获奖级别及人数进行调整，如下表：

    获奖级别一等奖二等奖三等奖
    调整前人数（单位：个）51530
    调整后人数（单位：个）m20n

    注：调整后增加一等奖人数，且学校购买奖品的预算经费控制在2050元之内.

    素材3

    调整后开始采购，了解到A，B两家超市均在搞促销活动.A超市买4盒水笔送1本笔记本，B超市所有商品九折出售.

    问题解决

    任务1

    探求商品单价

    请运用适当方法，求出每盒水笔和每本笔记本的价格.

    任务2

    探究设奖方案

    求m，n所有可能的值.

    任务3

    选择最优方案

    选择去哪家超市购买比较合算，请说明理由.

    查看试题解析

  • 24. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AC=8，BC=6，E，F分别是直线AC，AB上的动点，连结EF.

    (1)、求CD的长.
    (2)、若点E在边AC上，且3AE=2CE，EF⊥AC，求证：CF平分∠ACD.
    (3)、是否存在点E，F，使得以C，E，F为顶点的三角形与△CDF全等?若不存在，请说明理由；若存在，求出所有符合条件的DF的长.

    查看试题解析