2013年高考理数真题试卷（上海卷）

试卷更新日期：2016-09-28 类型：高考真卷

进入出卷网下载

一、填空题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．

1. 计算： $\lim_{n \to \infty}$ $\frac{n + 20}{3 n + 13}$ = ．

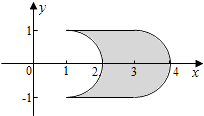
查看试题解析
2. 设m∈R，m²+m﹣2+（m²﹣1）i是纯虚数，其中i是虚数单位，则m= ．

查看试题解析
3. 若 $| \begin{matrix} x^{2} & y^{2} \\ - 1 & 1 \end{matrix} |$ = $| \begin{matrix} x & y \\ y & - y \end{matrix} |$ ，x+y= ．

查看试题解析
4. 已知△ABC的内角A、B、C所对的边分别是a、b、c，若3a²+2ab+3b²﹣3c²=0，则角C的大小是．

查看试题解析
5. 设常数a∈R，若 ${(x^{2} + \frac{a}{x})}^{5}$ 的二项展开式中x⁷项的系数为﹣10，则a= ．

查看试题解析
6. 方程 $\frac{3}{3^{x} - 1}$ + $\frac{1}{3}$ =3^x^﹣¹的实数解为．

查看试题解析
7. 在极坐标系中，曲线ρ=cosθ+1与ρcosθ=1的公共点到极点的距离为．

查看试题解析
8. 盒子中装有编号为1，2，3，4，5，6，7，8，9的九个球，从中任意取出两个，则这两个球的编号之积为偶数的概率是（结果用最简分数表示）．

查看试题解析
9. 设AB是椭圆Γ的长轴，点C在Γ上，且∠CBA= $\frac{π}{4}$ ，若AB=4，BC= $\sqrt{2}$ ，则Γ的两个焦点之间的距离为．

查看试题解析
10. 设非零常数d是等差数列x₁ ， x₂ ， …，x₁₉的公差，随机变量ξ等可能地取值x₁ ， x₂ ， …，x₁₉ ，则方差Dξ= ．

查看试题解析
11. 若cosxcosy+sinxsiny= $\frac{1}{2}$ ，sin2x+sin2y= $\frac{2}{3}$ ，则sin（x+y）= ．

查看试题解析
12. 设a为实常数，y=f（x）是定义在R上的奇函数，当x＜0时，f（x）=9x+ $\frac{a^{2}}{x}$ +7．若f（x）≥a+1对一切x≥0成立，则a的取值范围为．

查看试题解析
13. 在xOy平面上，将两个半圆弧（x﹣1）²+y²=1（x≥1）和（x﹣3）²+y²=1（x≥3），两条直线y=1和y=﹣1围成的封闭图形记为D，如图中阴影部分，记D绕y轴旋转一周而成的几何体为Ω．过（0，y）（|y|≤1）作Ω的水平截面，所得截面积为4π $\sqrt{1 - y^{2}}$ +8π．试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为．

查看试题解析
14. 对区间I上有定义的函数g（x），记g（I）={y|y=g（x），x∈I}．已知定义域为[0，3]的函数y=f（x）有反函数y=f^﹣¹（x），且f^﹣¹（[0，1））=[1，2），f^﹣¹（（2，4]）=[0，1）．若方程f（x）﹣x=0有解x₀ ，则x₀= ．

查看试题解析

二、选择题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．

15. 设常数a∈R，集合A={x|（x﹣1）（x﹣a）≥0}，B={x|x≥a﹣1}，若A∪B=R，则a的取值范围为（）

A、（﹣∞，2） B、（﹣∞，2] C、（2，+∞） D、[2，+∞）

查看试题解析
16. 钱大姐常说“便宜没好货”，她这句话的意思是：“不便宜”是“好货”的（）

A、充分条件 B、必要条件 C、充分必要条件 D、既非充分又非必要条件

查看试题解析
17. 在数列（a_n）中，a_n=2ⁿ﹣1，若一个7行12列的矩阵的第i行第j列的元素c_ij=a_i•a_j+a_i+a_j（i=1，2，…，7；j=1，2，…，12），则该矩阵元素能取到的不同数值的个数为（）

A、18 B、28 C、48 D、63

查看试题解析
18. 在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为 $\vec{a_{1}}$ 、 $\vec{a_{2}}$ 、 $\vec{a_{3}}$ 、 $\vec{a_{4}}$ 、 $\vec{a_{5}}$ ；以D为起点，其余顶点为终点的向量分别为 $\vec{d_{1}}$ 、 $\vec{d_{2}}$ 、 $\vec{d_{3}}$ 、 $\vec{d_{4}}$ 、 $\vec{d_{5}}$ ．若m、M分别为（ $\vec{a_{i}}$ + $\vec{a_{j}}$ + $\vec{a_{k}}$ ）•（ $\vec{d_{r}}$ + $\vec{d_{s}}$ + $\vec{d_{t}}$ ）的最小值、最大值，其中{i，j，k}⊆{1，2，3，4，5}，{r，s，t}⊆{1，2，3，4，5}，则m、M满足（）

A、m=0，M＞0 B、m＜0，M＞0 C、m＜0，M=0 D、m＜0，M＜0

查看试题解析

三、解答题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．

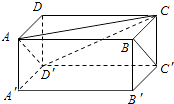
19. 如图，在长方体ABCD﹣A′B′C′D′中，AB=2，AD=1，AA′=1．证明直线BC′平行于平面D′AC，并求直线BC′到平面D′AC的距离．

查看试题解析
20. 甲厂以x千克/小时的速度匀速生产某种产品（生产条件要求1≤x≤10），每小时可获得的利润是100（5x+1﹣ $\frac{3}{x}$ ）元．

(1)、要使生产该产品2小时获得的利润不低于3000元，求x的取值范围；

(2)、要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求此最大利润．

查看试题解析
21. 已知函数f（x）=2sin（ωx），其中常数ω＞0

(1)、若y=f（x）在[﹣ $\frac{π}{4}$ ， $\frac{2 π}{3}$ ]上单调递增，求ω的取值范围；

(2)、令ω=2，将函数y=f（x）的图象向左平移 $\frac{π}{6}$ 个单位，再向上平移1个单位，得到函数y=g（x）的图象，区间[a，b]（a，b∈R，且a＜b）满足：y=g（x）在[a，b]上至少含有30个零点．在所有满足上述条件的[a，b]中，求b﹣a的最小值．

查看试题解析
22. 如图，已知双曲线C₁： $\frac{x^{2}}{2} - y^{2} = 1$ ，曲线C₂：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C₁ ， C₂都有公共点，则称P为“C₁﹣C₂型点”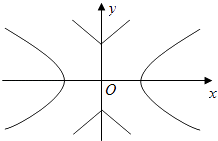

(1)、在正确证明C₁的左焦点是“C₁﹣C₂型点“时，要使用一条过该焦点的直线，试写出一条这样的直线的方程（不要求验证）；

(2)、设直线y=kx与C₂有公共点，求证|k|＞1，进而证明原点不是“C₁﹣C₂型点”；

(3)、求证：圆x²+y²= $\frac{1}{2}$ 内的点都不是“C₁﹣C₂型点”

查看试题解析
23. 给定常数c＞0，定义函数f（x）=2|x+c+4|﹣|x+c|．数列a₁ ， a₂ ， a₃ ， …满足a_n+1=f（a_n），n∈N^* ．

(1)、若a₁=﹣c﹣2，求a₂及a₃；

(2)、求证：对任意n∈N^* ， a_n+1﹣a_n≥c；

(3)、是否存在a₁ ，使得a₁ ， a₂ ， …，a_n ， …成等差数列？若存在，求出所有这样的a₁；若不存在，说明理由．

查看试题解析