湖南省长沙市重点中学2023-2024学年八年级上学期第三次月考数学试题
试卷更新日期:2024-01-18 类型:月考试卷
一、选择题(本题共10小题,每题3分)
-
1. 下列二次根式中,为最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 新型冠状病毒的直径大约为0.000000125米,0.000000125用科学记数法表示为( )A、 B、 C、 D、4. 下列式子从左到右的变形一定正确的是( )A、 B、 C、 D、5. 把分式中的x和y都扩大10倍,则分式的值( )A、扩大10倍 B、扩大100倍 C、缩小10倍 D、不变6. 如果是一个完全平方式,那么k的值是( )A、5 B、 C、10 D、7. 实数a、b在数轴上所对应的点如图所示,化简的结果是( )
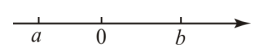 A、a B、 C、 D、8. 某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木,该活动开始后,实际每天比原计划每天多植树50棵,实际植树400棵所需时间与原计划植树300棵所需时间相同,设原计划每天植树x棵.则下列方程正确的是( )A、 B、 C、 D、9. 如图,已知锐角∠AOB,根据以下要求作图.
A、a B、 C、 D、8. 某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木,该活动开始后,实际每天比原计划每天多植树50棵,实际植树400棵所需时间与原计划植树300棵所需时间相同,设原计划每天植树x棵.则下列方程正确的是( )A、 B、 C、 D、9. 如图,已知锐角∠AOB,根据以下要求作图.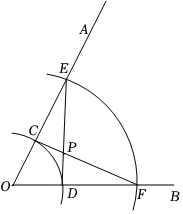
⑴在射线OA上取点C和点E,以点O为圆心,OC,OE的长为半径画弧,分别交射线OB于点D,F;
⑵连接CF,DE交于点P.
则下列结论错误的是( )
A、CE=DF B、点P在∠AOB的平分线上 C、PE=PF D、若∠AOB=60°,则∠CPD=120°10. 若分式方程的解为负数,则a的取值范围是( )A、且 B、且 C、且 D、且二、填空题(本题共6小题,每题3分)
-
11. 平面直角坐标系中,点关于y轴的对称点的坐标是 .12. 若二次根式 在实数范围内有意义,则x的取值范围为 .13. 因式分解: =.14. 如图,在中, , DE垂直平分AB , 分别交BC , AB于点D , E , 若 , 则 .
 15. 如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为.
15. 如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为.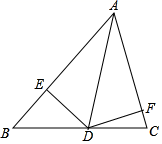 16. 已知 , 则代数式值= .
16. 已知 , 则代数式值= .三、解答题(本题共9小题)
-
17. 计算: .18. 先化简,再求代数式的值,其中 .19. 在平面直角坐标系中,的三个顶点均在正方形网格的格点上.
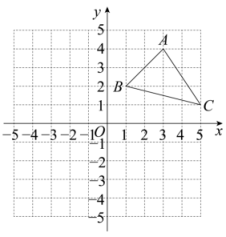 (1)、请你画出关于x轴的对称图形;(2)、求的面积;(3)、请你在y轴上找到一点P , 使得最小.20. 已知: , 求下列代数式的值:(1)、;(2)、 .21. 如图,在和中, , , , 且点D在线段上,连 .
(1)、请你画出关于x轴的对称图形;(2)、求的面积;(3)、请你在y轴上找到一点P , 使得最小.20. 已知: , 求下列代数式的值:(1)、;(2)、 .21. 如图,在和中, , , , 且点D在线段上,连 .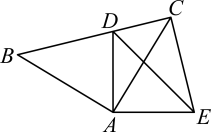 (1)、求证:;(2)、若 , 求的度数.22. 为培养大家的阅读能力,我校初一年级购进《朝花夕拾》和《西游记》两种书籍,花费分别是14000元和7000元,已知《朝花夕拾》的订购单价是《西游记》的订购单价的1.4倍,并且订购的《朝花夕拾》的数量比《西游记》的数量多300本.(1)、求我校初一年级订购的两种书籍的单价分别是多少元;(2)、我校初一年级某班计划再订购这两种书籍共10本来备用,其中《朝花夕拾》订购数量不低于3本,且两种书总费用不超过124元,求这个班订购这两种书籍有多少种方案?按照这些方案订购最低总费用为多少元?23. 利用所学知识计算:(1)、已知 , 且 , 求的值;(2)、已知a、b、c是等腰的三边长,若 , 求的周长.24. 如果两个分式M与N的和为常数k , 且k为正整数,则称M与N互为“和整分式常数k称为“和整值”如分式 , 则M与N互为“和整分式”,“和整值” .(1)、已知分式 , 判断A与B是否互为“和整分式”,若不是,请说明理由;若是,请求出“和整值”k;(2)、已知分式 , C与D互为“和整分式”,且“和整值” , 若x为正整数,分式D的值为正整数t .
(1)、求证:;(2)、若 , 求的度数.22. 为培养大家的阅读能力,我校初一年级购进《朝花夕拾》和《西游记》两种书籍,花费分别是14000元和7000元,已知《朝花夕拾》的订购单价是《西游记》的订购单价的1.4倍,并且订购的《朝花夕拾》的数量比《西游记》的数量多300本.(1)、求我校初一年级订购的两种书籍的单价分别是多少元;(2)、我校初一年级某班计划再订购这两种书籍共10本来备用,其中《朝花夕拾》订购数量不低于3本,且两种书总费用不超过124元,求这个班订购这两种书籍有多少种方案?按照这些方案订购最低总费用为多少元?23. 利用所学知识计算:(1)、已知 , 且 , 求的值;(2)、已知a、b、c是等腰的三边长,若 , 求的周长.24. 如果两个分式M与N的和为常数k , 且k为正整数,则称M与N互为“和整分式常数k称为“和整值”如分式 , 则M与N互为“和整分式”,“和整值” .(1)、已知分式 , 判断A与B是否互为“和整分式”,若不是,请说明理由;若是,请求出“和整值”k;(2)、已知分式 , C与D互为“和整分式”,且“和整值” , 若x为正整数,分式D的值为正整数t .①求G所代表的代数式:
②求x的值:
(3)、在(2)的条件下,已知分式 , 且 , 若该关于x的方程无解,求实数m的值.25. 在平面直角坐标系中,点A为y轴正半轴上一点,点B为x轴上一动点,连接AB , 以AB为腰作等腰 .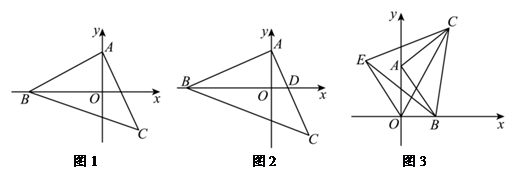 (1)、如图1,点B在x轴负半轴上,点C的坐标是 , 求点A和点B的坐标;(2)、如图2,点B在x轴负半轴上,AC交x轴于点D , 若BD平分 , 且点C的纵坐标是 , 求线段BD的长;(3)、如图3,点B在x轴正半轴上,以BC为边在BC左侧作等边 , 连接EO , CO , 若 , 且 , 求的面积.
(1)、如图1,点B在x轴负半轴上,点C的坐标是 , 求点A和点B的坐标;(2)、如图2,点B在x轴负半轴上,AC交x轴于点D , 若BD平分 , 且点C的纵坐标是 , 求线段BD的长;(3)、如图3,点B在x轴正半轴上,以BC为边在BC左侧作等边 , 连接EO , CO , 若 , 且 , 求的面积.