吉林省白山市浑江区2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-01-18 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 下列四个交通标志图案不是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为 盎司 将 用科学记数法表示为A、 B、 C、 D、3. 下列长度的三根木条首尾相连,能组成三角形的是( )A、10,7,5 B、10,7,3 C、10,5,3 D、4,4,104. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在和中,已知.在不添加任何辅助线的前提下,要使 , 只需再添加的一个条件不可以是( )
A、1个 B、2个 C、3个 D、4个2. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为 盎司 将 用科学记数法表示为A、 B、 C、 D、3. 下列长度的三根木条首尾相连,能组成三角形的是( )A、10,7,5 B、10,7,3 C、10,5,3 D、4,4,104. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在和中,已知.在不添加任何辅助线的前提下,要使 , 只需再添加的一个条件不可以是( ) A、 B、 C、 D、6. 使分式有意义的x的取值范围是( )A、 B、 C、 D、7. 若一个多边形的内角和与它的外角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形8. 如果x2+2mx+9是一个完全平方式,则m的值是( )
A、 B、 C、 D、6. 使分式有意义的x的取值范围是( )A、 B、 C、 D、7. 若一个多边形的内角和与它的外角和相等,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形8. 如果x2+2mx+9是一个完全平方式,则m的值是( )
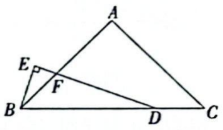
A、3 B、±3 C、6 D、±69. 如图,是的角平分线,于点E , , , , 则的长是( ) A、9 B、8 C、7 D、610. 甲、乙两人骑自行车从相距s千米的两地同时出发,若同向而行,经过a小时甲追上乙;若相向而行,经过b小时甲、乙相遇.设甲的速度为千米/时,乙的速度为千米/时,则等于( )A、 B、 C、 D、
A、9 B、8 C、7 D、610. 甲、乙两人骑自行车从相距s千米的两地同时出发,若同向而行,经过a小时甲追上乙;若相向而行,经过b小时甲、乙相遇.设甲的速度为千米/时,乙的速度为千米/时,则等于( )A、 B、 C、 D、二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 点关于x轴对称的点的坐标是.12. 如图,方格纸中是9个完全相同的小正方形,则的值为.
 13. 如图,在中, , 的垂直平分线交于点E , 垂足为D.若 , 则的长为.
13. 如图,在中, , 的垂直平分线交于点E , 垂足为D.若 , 则的长为. 14. 等腰三角形的一边长等于4,一边长等于9,它的周长是.15. 如图1是长方形纸带, , 将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是.
14. 等腰三角形的一边长等于4,一边长等于9,它的周长是.15. 如图1是长方形纸带, , 将纸带沿折叠成图2,再沿折叠成图3,则图3中的的度数是.
三、解答题(本大题共8个小题,共75分)
-
16.(1)、分解因式:.(2)、计算:.17. 如图, , , .求证:.
 18. 如图,是等边三角形,是中线,延长到点E , 使.求证:.
18. 如图,是等边三角形,是中线,延长到点E , 使.求证:. 19. 已知 , , 当时,求A的值.20. 如图,在中,AB的垂直平分线分别交AB , BC于点D , E , AC的垂直平分线分别交AC , BC于点F , G , 连接AE , AG.
19. 已知 , , 当时,求A的值.20. 如图,在中,AB的垂直平分线分别交AB , BC于点D , E , AC的垂直平分线分别交AC , BC于点F , G , 连接AE , AG. (1)、若的周长为10,求线段BC的长;(2)、若 , 求的度数.21. 某企业有甲、乙两个车间用于生产医用防护服.甲车间每天生产的数量是乙车间每天生产数量的1.5倍,两车间各加工6000套医用防护服,甲车间比乙车间少用4天.(1)、甲、乙两车间每天各生产多少套医用防护服?(2)、已知甲、乙两车间生产这种医用防护服每天的生产费用分别是12000元和10000元,现有18000套医用防护服的生产任务,甲车间单独生产一段时间后另有安排,剩余任务由乙车间单独完成.如果总生产费用不超过339000元,则甲车间至少需要生产几天?
(1)、若的周长为10,求线段BC的长;(2)、若 , 求的度数.21. 某企业有甲、乙两个车间用于生产医用防护服.甲车间每天生产的数量是乙车间每天生产数量的1.5倍,两车间各加工6000套医用防护服,甲车间比乙车间少用4天.(1)、甲、乙两车间每天各生产多少套医用防护服?(2)、已知甲、乙两车间生产这种医用防护服每天的生产费用分别是12000元和10000元,现有18000套医用防护服的生产任务,甲车间单独生产一段时间后另有安排,剩余任务由乙车间单独完成.如果总生产费用不超过339000元,则甲车间至少需要生产几天?