吉林省白山市临江市2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-01-18 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 下面四个标志,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长分别为3 cm和4 cm,则该三角形第三边的长不可能是( )A、1 cm B、3 cm C、5 cm D、6 cm3. 1nm为十亿分之一米,而个体中红细胞的直径约为0.0000077m , 那么人体中红细胞直径的纳米数用科学记数法表示为( )A、7.7×103nm B、7.7×102nm C、7.7×104nm D、以上都不对4. 若点 与 关于 轴对称,则( )A、 , B、 , C、 , D、 ,5. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C , 在△ABC中, , 则∠A的度数是( )
2. 已知三角形的两边长分别为3 cm和4 cm,则该三角形第三边的长不可能是( )A、1 cm B、3 cm C、5 cm D、6 cm3. 1nm为十亿分之一米,而个体中红细胞的直径约为0.0000077m , 那么人体中红细胞直径的纳米数用科学记数法表示为( )A、7.7×103nm B、7.7×102nm C、7.7×104nm D、以上都不对4. 若点 与 关于 轴对称,则( )A、 , B、 , C、 , D、 ,5. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C , 在△ABC中, , 则∠A的度数是( )
 A、 B、 C、 D、6. 计算 的结果正确的是( )A、 B、 C、 D、7. 生活垃圾通常可分为厨余垃圾、可回收物、有害垃圾和其他垃圾.某小区去年5月和12月的厨余垃圾分出量与其他三种垃圾的总量的相关信息如下表所示:
A、 B、 C、 D、6. 计算 的结果正确的是( )A、 B、 C、 D、7. 生活垃圾通常可分为厨余垃圾、可回收物、有害垃圾和其他垃圾.某小区去年5月和12月的厨余垃圾分出量与其他三种垃圾的总量的相关信息如下表所示:月份
类别
5月
12月
厨余垃圾分出量()
660
8400
其他三种垃圾的总量()
x
如果厨余垃圾分出率(生活垃圾总量=厨佘垃圾分出量+其他三种垃圾的总量),且该小区12月的厨余垃圾分出率是5月的厨余垃圾分出率的14倍,则下列方程正确的是( )
A、 B、 C、 D、8. 设a , b是任意有理数,定义一种新运算: . 下面有四个推断:①;②;③;④ , 其中正确的序号是( )A、①②③④ B、①③④ C、①② D、①③9. 已知AD是△ABC的边BC上的中线,AB=12,AC=8,则中线AD的取值范围是( )A、2<AD<10 B、4<AD<20 C、1<AD<4 D、以上都不对10. 如图,任意画一个的 , 再分别作的两条角平分线和 , 和相交于点 , 连接 , 有以下结论:①;②平分;③;④;⑤ , 正确的有( )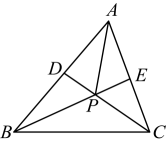 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 若分式在实数范围内有意义,则实数x的取值范围是 .12. 在平面直角坐标系中,点关于x轴的对称点的坐标为 .13. 若关于x的方程的解是非负数,则m的取值范围是 .14. 如图所示的四边形均为长方形,请写出一个可以用图中图形的面积关系说明的正确等式 .
 15. 如图,AD是ABC的角平分线,DE⊥AC , 垂足为E , BFAC交ED的延长线于点F , BC恰好平分∠ABF , AE=2BF . 若CE=2,则AB= .
15. 如图,AD是ABC的角平分线,DE⊥AC , 垂足为E , BFAC交ED的延长线于点F , BC恰好平分∠ABF , AE=2BF . 若CE=2,则AB= .
三、解答题(本大题共8个小题,共75分)
-
16. 解方程:(1)、;(2)、 .17. 先化简,再求值: , 其中x从0,1,2中取一个合适的数求值.18. 分解因式(1)、(2)、19. 计算(1)、(2)、20.(1)、如图1,在中,分别平分和 , 请直接写出与的数量关系: .
 (2)、如图2,在四边形中,分别平分和 , 试探究与的数量关系,并说明理由.
(2)、如图2,在四边形中,分别平分和 , 试探究与的数量关系,并说明理由. 21. 如图,中, , 点分别在边上, , .
21. 如图,中, , 点分别在边上, , .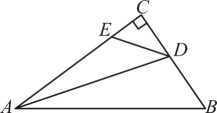 (1)、求证:平分;(2)、写出与的数量关系,并说明理由.22. 下面是小明设计的“作一个含角的直角三角形”的尺规作图过程.
(1)、求证:平分;(2)、写出与的数量关系,并说明理由.22. 下面是小明设计的“作一个含角的直角三角形”的尺规作图过程.已知:如图,直线及直线上一点 .

求作: , 使得 , .

作法:如图,
①在直线上取点;
②分别以点为圆心,长为半径画弧,交于点;
③作直线 , 交直线于点;
④连接 .
就是所求作的三角形.
根据小明设计的尺规作图过程,
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明:证明:连接 , , .
,
是等边三角形.
.
▲
点在线段的垂直平分线上(①▲ )(填推理的依据).
.
.
(②▲ )(填推理的依据).
.
23. 如图,是的高,点在的延长线上, , 点在上, .
 (1)、判断:(选填“”“”或“=”);(2)、探究与之间的关系,并说明理由;(3)、若把题中的改为钝角三角形, , 是钝角,其他条件不变,试探究与之间的关系,请画出图形并写出结论.
(1)、判断:(选填“”“”或“=”);(2)、探究与之间的关系,并说明理由;(3)、若把题中的改为钝角三角形, , 是钝角,其他条件不变,试探究与之间的关系,请画出图形并写出结论.