湖南省娄底市涟源市2023-2024学年九年级上学期月考数学试题

试卷更新日期：2024-01-18 类型：月考试卷

进入出卷网下载

一、选择题（在下列各题的四个选项中，只有一项是符合题意的，请在答题卡中填涂符合题意的选项，本大题共10个小题，每小题3分，共30分）

1. 将一元二次方程 $2 x^{2} - 7 x = 10$ 化成一般形式后，其中的二次项系数，一次项系数，常数项分别是（）

A、 $- 2 ， 7 ， - 10$ B、 $2 ， - 7 ， 10$ C、 $- 2 ， - 7 ， 10$ D、 $2 ， - 7 ， - 10$

查看试题解析
2. 下列一元二次方程有实数根的是（）

A、 $x^{2} + x + 1 = 0$ B、 $x^{2} + 4 = 0$ C、 $x^{2} + x = 0$ D、 $2 x^{2} + 3 x + 2 = 0$

查看试题解析
3. 某山区为估计该山区鸟的只数，先捕捉40只鸟给它们分别作上标志，然后放回，待有标志的鸟完全混合于鸟群后，第二次捕捉120只鸟，发现其中4只有标志．从而估计该地区有鸟（）

A、800只 B、1200只 C、1600只 D、2000只

查看试题解析
4. 在 $R t △ A B C$ 中， $∠ C = 90 ° ， B C = 3 ， A B = 4$ ，那么下列结论正确的是（）

A、 $c o s A = \frac{4}{5}$ B、 $s i n A = \frac{3}{4}$ C、 $t a n B = \frac{4}{3}$ D、 $t a n A = \frac{3}{4}$

查看试题解析
5. 某反比例函数图象上四个点的坐标分别为 $(- 3 ， y_{1}) ， (- 2 ， 3) ， (1 ， y_{2}) ， (2 ， y_{3})$ ，则， $y_{1} ， y_{2} ， y_{3}$ 的大小关系为（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
6. 如图，P是叶脉AB的黄金分割点（ $P A > P B$ ），则 $\frac{P B}{A P} =$ （）

A、 $\frac{A P}{A B}$ B、 $\frac{A B}{B P}$ C、 $\frac{A P}{B P}$ D、 $\frac{A P^{2}}{A B^{2}}$

查看试题解析
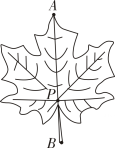7. 如图，两个反比例函数 $y = \frac{14}{x}$ 和 $y = \frac{8}{x}$ 在第一象限内的图象分别是 $C_{1}$ 和 $C_{2}$ ，设点 $P$ 在 $C_{1}$ 上， $P A ⊥ x$ 轴于点 $A$ ，交 $C_{2}$ 于点 $B$ ，则 $△ P O B$ 的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，它是物理学中小孔成像的原理示意图，已知物体 $A B = 30$ ，根据图中尺寸 $(A B ∥ C D)$ ，则 $C D$ 的长应是（）

A、15 B、30 C、20 D、10

查看试题解析
9. 如图是冬奥会首钢滑雪大跳台赛道的剖面图，剖面图的一部分可抽象为线段 $A B$ ．已知斜坡 $A B$ 的坡比接近 $3 ： 4$ ，坡长 $A B$ 为 $n$ 米，则坡 $A B$ 的铅垂高度 $A H$ 约为（）米．

A、 $\frac{n}{3}$ B、 $\frac{\sqrt{7} n}{7}$ C、 $\frac{4 n}{5}$ D、 $\frac{3 n}{5}$

查看试题解析
10. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = (2 a x_{0} + b)^{2}$ ；⑤存在实数 $m ， n (m \neq n)$ ，使得 $a m^{2} + b m + c = a n^{2} + b n + c$ ．
其中正确的（）

A、只有①②④ B、只有①②④⑤ C、①②③④⑤ D、只有①②③

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

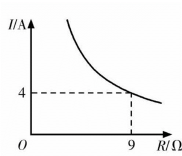
11. 已知蓄电池的电压恒定，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，流过的电流是2A，那么此用电器的电阻是Ω.

查看试题解析
12. 关于 $x$ 的一元二次方程 $x^{2} + m x - 3 = 0$ 的一个根是 $- 3$ ，则它的另一个根是．

查看试题解析
13. 若锐角 $x$ 满足 $c o s (x - 10 °) = \frac{\sqrt{3}}{2}$ ，则 $x$ 为．

查看试题解析
14. 如图，在平面直角坐标系中， $△ A O B$ 与 $△ C O D$ 是以点 $O$ 为位似中心的位似图形，若 $A (3 ， 0) ， B (2 ， - 1) ， C (6 ， 0)$ ，则点 $B$ 的对应点 $D$ 的坐标为．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = 5 ， B C = 12 ， C D ⊥ A B$ 于点 $D$ ，则 $c o s ∠ A C D$ 的值为．

查看试题解析
16. 如图，正方形 $A B C D$ 中， $E 、 F$ 分别在边 $A D 、 C D$ 上， $A F 、 B E$ 相交于点 $G$ ，若 $A D = 3 A E ， D F = C F$ ，则 $\frac{A G}{G F}$ 的值是．

查看试题解析

三、解答题（本大题共9个小题，第17、18、19题每题6分，第20、21题每题8分，第22、23题每题9分，第24、25题每题10分，共72分，解答应写出必要的文字说明、证明过程或演算步骤）

17. 计算： ${(\frac{1}{2})}^{- 1} - (2023 - π)^{0} + | \sqrt{3} - 2 | + 2 s i n 60 °$ ．

查看试题解析
18. 已知反比例函数 $y = \frac{k - 4}{x}$ 的图象位于第一、三象限．

(1)、求 $k$ 的取值范围；

(2)、若 $k = 6$ ，反比例函数的图象过点 $A (2 ， m)$ ，求 $m$ 的值．

查看试题解析
19. 先化简，再求值 $(x - \frac{3 x}{x + 2}) \div \frac{x}{x^{2} + 4 x + 4}$ ，其中 $x$ 满足 $x^{2} + 2 x - 3 = 0$ ．

查看试题解析
20. 2023年，教育部等八部门联合印发了《全国青少年学生读书行动实施方案》，某校为落实该方案，成立了四个主题阅读社团：A．民俗文化，B．节日文化，C．古典诗词．D．红色经典．学校规定：每名学生必须参加且只能参加其中一个社团，学校随机对部分学生选择社团的情况进行了调查．下面是根据调查结果绘制的两幅不完整的统计图．
请根据图中提供的信息，解答下列问题：

(1)、本次随机调查的学生有名，在扇形统计图中“A”部分圆心角的度数为；

(2)、通过计算补全条形统计图；

(3)、若该校共有1800名学生，请根据以上调查结果，估计全校参加“D”社团的人数．

查看试题解析
21. 三晋名刹双塔寺，本名“永祚寺”，位于山西省太原市城区东南方向，距市中心4公里左右的郝庄村南之向山脚畔，这里绿树红墙，宝塔梵殿，碑碣栉比，花卉溢香，松柏凝翠，古香古色.数学兴趣小组在周末时间参观了双塔寺，对寺内“舍利塔”的高度做了测量，如图所示，点 $A$ 为塔底中心点，观测者小明在点 $D$ 测得塔顶 $B$ 的仰角为 $30 °$ ，沿着 $D A$ 向前走40米到达点 $C$ ，此时测得塔顶 $B$ 的仰角为 $45 °$ ，测量时点 $A ， C ， D$ 在同一水平直线上，且与点 $B$ 在同一竖直平面内，根据该小组所获得的数据，请你求出塔 $A B$ 高度是多少？（结果精确到整数，参考数据， $\sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ ）

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B = 90 ° ， A B = 5 c m ， B C = 8 c m$ ．点 $P$ 从点 $A$ 开始沿 $A B$ 边向点 $B$ 以 $1 c m / s$ 的速度移动，同时点 $Q$ 从点 $B$ 开始沿 $B C$ 边向点 $C$ 以 $2 c m / s$ 的速度移动，当其中一点到达终点时，另外一点也随之停止运动．

(1)、几秒后，四边形 $A P Q C$ 的面积等于 $16 c m^{2}$ ？

(2)、 $△ P Q B$ 的面积能否等于 $9 c m^{2}$ ？请说明理由．

查看试题解析
23. 如图．已知 $B D$ 是 $∠ A B C$ 的角平分线， $E$ 是 $B D$ 延长线上的一点且 $A E = A B$ ．

(1)、求证： $△ A D E ∽ △ C D B$ ；

(2)、若 $A B = 6 ， B D = 4 ， B E = 9$ ，求 $B C$ 的长．

查看试题解析
24. 如图，在菱形 $A B C D$ 中， $D E ⊥ B C$ 交 $B C$ 的延长线于点 $E$ ，连结 $A E$ 交 $B D$ 于点 $F$ ，交 $C D$ 于点 $G$ ，连结 $C F$ ．

(1)、求证： $A F = C F$ ；

(2)、求证： $A F^{2} = E F \cdot G F$ ；

(3)、若菱形 $A B C D$ 的边长为2， $∠ B A D = 120 °$ ，求 $F G$ 的长．

查看试题解析
25. 如图，在直角坐标系中，直线 $y = - \frac{1}{3} x$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A (m ， 1)$ 、 $B$ 两点．

(1)、求反比例函数的表达式；

(2)、求点B的坐标，并根据图象直接写出 $- \frac{1}{3} x < \frac{k}{x}$ 的解集；

(3)、将直线 $y = - \frac{1}{3} x$ 向上平移后与 $y$ 轴交于点 $C$ ，与双曲线在第二象限内的部分交于点 $D$ ，如果 $△ A B D$ 的面积为12，求平移后的直线表达式．

查看试题解析