河北省沧州市2023-2024学年八年级上学期第三次月考数学试题
试卷更新日期:2024-01-18 类型:月考试卷
一、选择题(本大题共16个小题,共38分.1~6小题各3分;7~16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列命题不正确的是( )A、从n边形的一个顶点出发,可以作条对角线 B、两个全等三角形对应边上的高相等 C、若两个三角形全等,则它们一定关于某条直线成轴对称 D、有两个内角分别为与的三角形是等腰三角形3. 已知点与点关于y轴对称,那么的值为( )A、1 B、2 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在中, , 是上两点,且 , 平分 , 那么下列说法中不正确的是( )
2. 下列命题不正确的是( )A、从n边形的一个顶点出发,可以作条对角线 B、两个全等三角形对应边上的高相等 C、若两个三角形全等,则它们一定关于某条直线成轴对称 D、有两个内角分别为与的三角形是等腰三角形3. 已知点与点关于y轴对称,那么的值为( )A、1 B、2 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在中, , 是上两点,且 , 平分 , 那么下列说法中不正确的是( )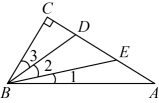 A、是的中线 B、是的角平分线 C、 D、是的高6. 如图, , 若要使 , 则添加的一个条件不能是( )
A、是的中线 B、是的角平分线 C、 D、是的高6. 如图, , 若要使 , 则添加的一个条件不能是( )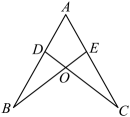 A、 B、 C、 D、7. 如图,与关于直线l对称,若 , , 则( )
A、 B、 C、 D、7. 如图,与关于直线l对称,若 , , 则( )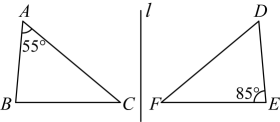 A、 B、 C、 D、8. 如图,在中, , , 是边上的高,的平分线交于点F , 交于点E , 则图中共有等腰三角形( )
A、 B、 C、 D、8. 如图,在中, , , 是边上的高,的平分线交于点F , 交于点E , 则图中共有等腰三角形( )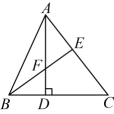 A、2个 B、3个 C、4个 D、5个9. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( )
A、2个 B、3个 C、4个 D、5个9. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( )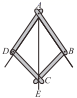 A、SSS B、ASA C、SAS D、AAS10. 如图,在中, , , , 直线m是中边的垂直平分线,交于点P , 则的周长为( )
A、SSS B、ASA C、SAS D、AAS10. 如图,在中, , , , 直线m是中边的垂直平分线,交于点P , 则的周长为( )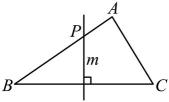 A、6 B、10 C、11 D、1311. 要使多项式不含x的一次项,则m的值为( )A、0 B、1 C、2 D、12. 下列轴对称图形中,对称轴条数最少的是( )A、等边三角形 B、正方形 C、正八边形 D、圆13. 在中, , , 尺规作图痕迹如图所示.结论Ⅰ:连接 , 则;结论Ⅱ:点F到三边距离相等.对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A、6 B、10 C、11 D、1311. 要使多项式不含x的一次项,则m的值为( )A、0 B、1 C、2 D、12. 下列轴对称图形中,对称轴条数最少的是( )A、等边三角形 B、正方形 C、正八边形 D、圆13. 在中, , , 尺规作图痕迹如图所示.结论Ⅰ:连接 , 则;结论Ⅱ:点F到三边距离相等.对于结论Ⅰ和Ⅱ,下列判断正确的是( )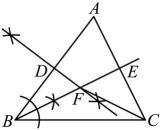 A、Ⅰ和Ⅱ都对 B、Ⅰ对、Ⅱ不对 C、Ⅱ对,Ⅰ不对 D、Ⅰ和Ⅱ都不对14. 如图,上午8时,一条船从海岛A出发,以20海里/时的速度向北航行,10时到达海岛B处,分别从A、B两海岛望灯塔C , 测得 , , 则从海岛B到灯塔C的距离为( )
A、Ⅰ和Ⅱ都对 B、Ⅰ对、Ⅱ不对 C、Ⅱ对,Ⅰ不对 D、Ⅰ和Ⅱ都不对14. 如图,上午8时,一条船从海岛A出发,以20海里/时的速度向北航行,10时到达海岛B处,分别从A、B两海岛望灯塔C , 测得 , , 则从海岛B到灯塔C的距离为( )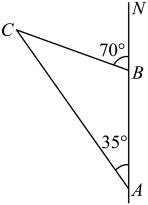 A、25海里 B、30海里 C、35海里 D、40海里15. 小明有足够多的如图所示的正方形卡片 , 和长方形卡片 , 如果他要拼一个长为 , 宽为的大长方形,共需要类卡片( )
A、25海里 B、30海里 C、35海里 D、40海里15. 小明有足够多的如图所示的正方形卡片 , 和长方形卡片 , 如果他要拼一个长为 , 宽为的大长方形,共需要类卡片( )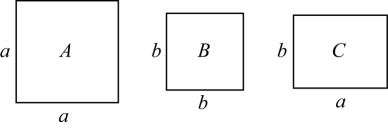 A、3张 B、4张 C、5张 D、6张16. 如图,在中, , , , 点P从点B出发以每秒的速度向点A运动,点Q从点A同时出发以每秒的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒,当为直角三角形时,t的值为( )
A、3张 B、4张 C、5张 D、6张16. 如图,在中, , , , 点P从点B出发以每秒的速度向点A运动,点Q从点A同时出发以每秒的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒,当为直角三角形时,t的值为( )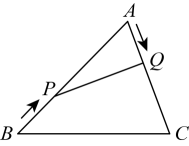 A、秒 B、3秒 C、或3秒 D、3或秒
A、秒 B、3秒 C、或3秒 D、3或秒二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分,把答案写在题中横线上)
-
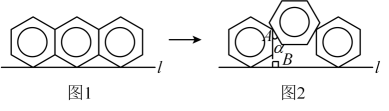
17. 已知 , 则 .18. 将三个相同的六角形螺母并排摆放在桌面上,从上面看到的图形如图1所示,正六边形边长为3且各有一个顶点在直线l上,则图1中螺母组成的图形的周长(图中加粗部分总长度)为;两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看到的图形如图11-2所示,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点,正六边形边直线l . 则 .
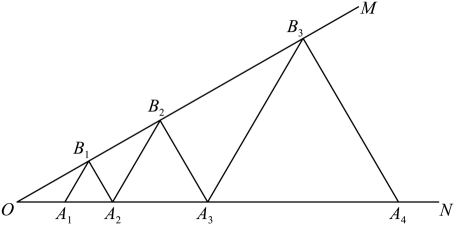
 19. 如图,已知 , 点 , , , …在射线上,点 , , , …在射线上, , , , …均为等边三角形,若 , 则 , , ……
19. 如图,已知 , 点 , , , …在射线上,点 , , , …在射线上, , , , …均为等边三角形,若 , 则 , , ……⑴的边长为;⑵的边长为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 已知关于x的多项式M , 当时,完成下列各题:(1)、求多项式M;(2)、①若 , 求多项式M的值;
②若 , 求多项式M的值.
21. 已知的三边分别为a、b、c , 且 .(1)、求a , c的值;(2)、若b为奇数,求的周长.22. 如图,在中,和的平分线交于点E , 过点E作交于点M , 交于点N , 若 , .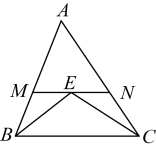 (1)、求证:;(2)、求的周长.23. 发现:两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为这两个正整数的平方和.(1)、验证:如,为偶数,请把20的一半表示为两个正整数的平方和.(2)、探究:设“发现”中的两个已知正整数为a、b , 请论证“发现”中的结论正确.24. 如图,在所给网格图(每小格均为边长是1的正方形,每个小正方形的顶点称为格点)中完成下列各题:
(1)、求证:;(2)、求的周长.23. 发现:两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为这两个正整数的平方和.(1)、验证:如,为偶数,请把20的一半表示为两个正整数的平方和.(2)、探究:设“发现”中的两个已知正整数为a、b , 请论证“发现”中的结论正确.24. 如图,在所给网格图(每小格均为边长是1的正方形,每个小正方形的顶点称为格点)中完成下列各题: (1)、画出格点(顶点均在格点上)关于直线对称的图形;(2)、在上画出点P , 使最小;(3)、在上画出点Q , 使Q到B , C两点的距离相等;(4)、四边形的面积为 .25. 如图,和关于直线对称,和关于直线对称.
(1)、画出格点(顶点均在格点上)关于直线对称的图形;(2)、在上画出点P , 使最小;(3)、在上画出点Q , 使Q到B , C两点的距离相等;(4)、四边形的面积为 .25. 如图,和关于直线对称,和关于直线对称.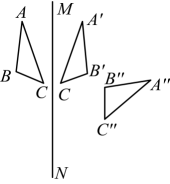 (1)、作出直线(尺规作图,不写作法,保留作图痕迹);(2)、直线与相交于点O , 且直线 , 所夹锐角 , 求的度数;(3)、在(2)的条件下,小颖得出 , 请你运用所学知识判断小颖的结论是否正确,并说明理由.26. 如图,在平面直角坐标系中,点B的坐标为 , 以线段为边在第一象限内作等边 , 动点D从点B出发以每秒1个单位长度的速度从左向右在x轴正半轴上运动,设运动时间为t秒.连接 , 以线段为边在第一象限内作等边 , 连接并延长,交y轴于点E .
(1)、作出直线(尺规作图,不写作法,保留作图痕迹);(2)、直线与相交于点O , 且直线 , 所夹锐角 , 求的度数;(3)、在(2)的条件下,小颖得出 , 请你运用所学知识判断小颖的结论是否正确,并说明理由.26. 如图,在平面直角坐标系中,点B的坐标为 , 以线段为边在第一象限内作等边 , 动点D从点B出发以每秒1个单位长度的速度从左向右在x轴正半轴上运动,设运动时间为t秒.连接 , 以线段为边在第一象限内作等边 , 连接并延长,交y轴于点E .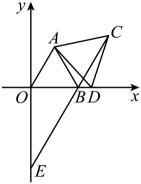 (1)、求证:;(2)、在点D的运动过程中,的度数是否会变化?如果不变,请求出的度数;如果变化,请说明理由.(3)、当t为何值时,以B , E , D为顶点的三角形是等腰三角形?
(1)、求证:;(2)、在点D的运动过程中,的度数是否会变化?如果不变,请求出的度数;如果变化,请说明理由.(3)、当t为何值时,以B , E , D为顶点的三角形是等腰三角形?