山西省朔州市怀仁市2023-2024学年九年级上学期期中数学试题
试卷更新日期:2024-01-18 类型:期中考试
一、选择题(本大题共10小题,每题3分,总共30分,在每小题给出的四个选项中只有一项是符合题目要求,请选出并在答题卡上将该项涂黑)
-
1. 为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若三角形三边的长均能使代数式 的值为零,则此三角形的周长是( )A、9或18 B、12或15 C、9或15或18 D、9或12或153. 如图,为⊙的直径,点在圆上且在直径的两侧,若 , 则的度数为( )
2. 若三角形三边的长均能使代数式 的值为零,则此三角形的周长是( )A、9或18 B、12或15 C、9或15或18 D、9或12或153. 如图,为⊙的直径,点在圆上且在直径的两侧,若 , 则的度数为( )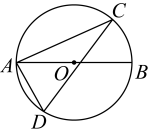 A、 B、 C、 D、4. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、
A、 B、 C、 D、4. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、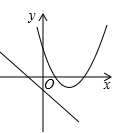 B、
B、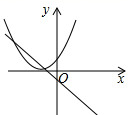 C、
C、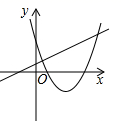 D、
D、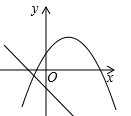 5. 配方法是解一元二次方程的一种基本方法,其本质是将一元二次方程由一般式化为的形式,然后利用开方求一元二次方程的解的过程,这个过程体现的数学思想是( )A、数形结合思想 B、函数思想 C、转化思想 D、公理化思想6. 如图,在中, , 将绕点逆时针旋转到的位置,使得 , 则的度数是( )
5. 配方法是解一元二次方程的一种基本方法,其本质是将一元二次方程由一般式化为的形式,然后利用开方求一元二次方程的解的过程,这个过程体现的数学思想是( )A、数形结合思想 B、函数思想 C、转化思想 D、公理化思想6. 如图,在中, , 将绕点逆时针旋转到的位置,使得 , 则的度数是( ) A、 B、 C、 D、7. 将抛物线先向右平移3个单位长度,再向下平移1个单位长度,所得到的抛物线解析式为( )A、 B、 C、 D、8. 如图, , 分别切于点A , B , 点C在上,若四边形为菱形,则为( )
A、 B、 C、 D、7. 将抛物线先向右平移3个单位长度,再向下平移1个单位长度,所得到的抛物线解析式为( )A、 B、 C、 D、8. 如图, , 分别切于点A , B , 点C在上,若四边形为菱形,则为( )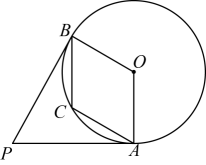 A、 B、 C、 D、9. 在研究二次函数时,下面是某小组列出的部分和的对应值:
A、 B、 C、 D、9. 在研究二次函数时,下面是某小组列出的部分和的对应值:…
1
…
…
8
8
…
根据表格可知,下列说法中错误的是( )
A、该二次函数图象的对称轴是直线 B、关于的方程的解是 , C、的最大值是8 D、的值是10. 如图是某公园在一长 , 宽的矩形湖面上修建的等宽的人行观景曲桥,它的面积恰好为原矩形湖面面积的 , 求人行观景曲桥的宽.若设人行观景曲桥的宽为 , 则满足的方程为( )
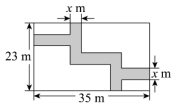 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分共15分)
-
11. 若关于x的方程有两个相等的实数根,则的值为 .12. 若点三点在抛物线的图象上,则的大小关系是(用“<”连接).13. 如图, 是 的两条相交弦, ,则 的直径是 .
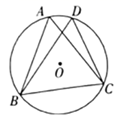 14. 如图,抛物线与直线的两个交点坐标分别为 , , 则不等式的解集是 .
14. 如图,抛物线与直线的两个交点坐标分别为 , , 则不等式的解集是 .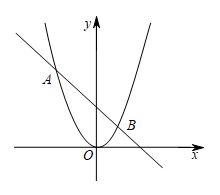 15. 如图,某同学拿着含角的直角三角板绕点C逆时针旋转得到 , 连结 , 与AC相交于点O . 已知 , 则OC的长为 .
15. 如图,某同学拿着含角的直角三角板绕点C逆时针旋转得到 , 连结 , 与AC相交于点O . 已知 , 则OC的长为 .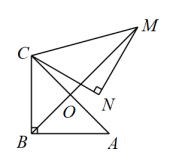
三、解答题(本大题共8个小题,共75分解答应写出文字说明,证明过程或演算步骤)
-
16. 解下列方程(1)、;(2)、17. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
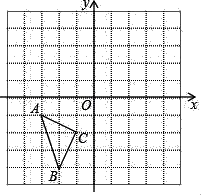 (1)、以O为中心作出△ABC的中心对称图形△A1B1C1 , 并写出点B1坐标;(2)、以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.18. 阅读理解,并解决问题:
(1)、以O为中心作出△ABC的中心对称图形△A1B1C1 , 并写出点B1坐标;(2)、以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.18. 阅读理解,并解决问题:“整体思想”是中学数学中的一种重要思想,贯穿于中学数学的全过程,比如整体代入,整体换元,整体约减,整体求和,整体构造,…,有些问题若从局部求解,采取各个击破的方式,很难解决,而从全局着眼,整体思考,会使问题化繁为简,化难为易,复杂问题也能迎刃而解.
例:当代数式 的值为7时,求代数式 的值.
解:因为 ,所以 .
所以.
以上方法是典型的整体代入法.
请根据阅读材料,解决下列问题:
(1)、已知 ,求 的值.(2)、我们知道方程 的解是 ,现给出另一个方程 ,则它的解是 .19. 如图,是的外接圆,是的直径,过O作于点E , 延长至点D , 连接 , 使 .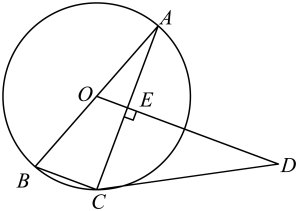 (1)、求证:是的切线;(2)、若 , 求的长.20. 太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.(1)、求每天的销售量y(件)关于x(元)的函数关系式.(2)、在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.21. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为 , 当水平距离为3m时,实心球行进至最高点3m处.
(1)、求证:是的切线;(2)、若 , 求的长.20. 太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.(1)、求每天的销售量y(件)关于x(元)的函数关系式.(2)、在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.21. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为 , 当水平距离为3m时,实心球行进至最高点3m处.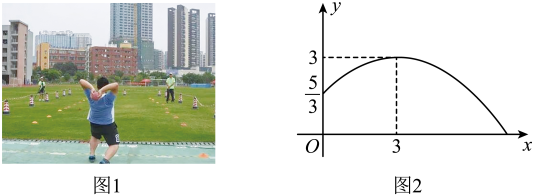 (1)、求y关于x的函数表达式;(2)、根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.22. 综合与实践
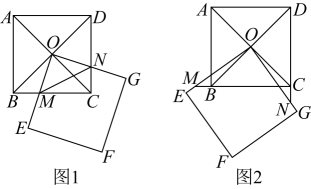
(1)、求y关于x的函数表达式;(2)、根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.22. 综合与实践问题情境:在综合实践课上,李老师让同学们根据如下问题情境,写出两个数学结论:如图1,正方形的对角线交于点O , 点O又是正方形的一个顶点(正方形 的边长足够长),将正方形绕点O做旋转实验,与交于点M , 与交于点N.如图1“求实小组”写出的两个数学结论是:① ; ②.
 (1)、问题解决:
(1)、问题解决:请你证明“求实小组”所写的两个结论的正确性.
(2)、类比探究:如图2解决完“求实小组”的两个问题后,老师让同学们继续探究,再提出新的问题﹔如图2,将正方形在图1的基础上旋转一定的角度,当与的延长线交于点M , 与的延长线交于点N , 则“求实小组”所写的两个结论是否仍然成立?请说明理由.
23. 综合与探究如图,抛物线与轴交于两点(点在点的左侧),与轴交于点 , 点是第一象限内抛物线上的一个动点.
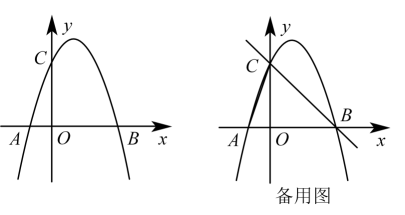 (1)、请直接写出点A , B , C的坐标;(2)、是否存在这样的点 , 使得?若存在,求出点的坐标;若不存在,请说明理由;(3)、若点是直线上一点,是否存在点 , 使得以点为顶点的三角形是等腰三角形?若存在,求出的坐标;若不存在,请说明理由.
(1)、请直接写出点A , B , C的坐标;(2)、是否存在这样的点 , 使得?若存在,求出点的坐标;若不存在,请说明理由;(3)、若点是直线上一点,是否存在点 , 使得以点为顶点的三角形是等腰三角形?若存在,求出的坐标;若不存在,请说明理由.