湖南省郴州市汝城县七中片区2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-01-18 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $(2，3)$ ，那么下列四个点中，也在这个函数图象上的是（）

A、 $(- 6，1)$ B、 $(1，6)$ C、 $(2 ， - 3)$ D、 $(3 ， - 2)$

查看试题解析
2. 从全市 $5000$ 份数学试卷中随机抽取 $400$ 份试卷，其中 $360$ 份成绩合格，那么可以估计全市数学成绩合格的学生大约有多少人？（）

A、 $4500$ B、 $4000$ C、 $3600$ D、 $4800$

查看试题解析
3. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

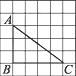查看试题解析
4. 一元二次方程x²－8x－1＝0配方后可变形为（）

A、（x＋4）²＝17 B、（x＋4）²＝15 C、（x－4）²＝17 D、（x－4）²＝15

查看试题解析
5. 关于二次函数 $y = (x - 1)^{2} + 5$ ，下列说法正确的是（）

A、函数图象的开口向下 B、函数图象的顶点坐标是 $(- 1，5)$ C、该函数有最大值，最大值是 $5$ D、当 $x > 1$ 时， $y$ 随 $x$ 的增大而增大

查看试题解析
6. 已知关于x的一元二次方程mx²+2x-1=0有两个不相等的实数根，则m的取值范围是（）

A、m<-1 B、m>1 C、m<1且m≠0 D、m>-1且m≠0

查看试题解析
7. $△ A B C$ 与 $△ D E F$ 是相似三角形，且 $△ A B C$ 与 $△ D E F$ 的相似比是 $1$ ： $2$ ，已知 $△ A B C$ 的面积是 $3$ ，则 $△ D E F$ 的面积是（）

A、 $3$ B、 $6$ C、 $9$ D、 $12$

查看试题解析
8. 如图是拦水坝的横断面，堤高 $B C$ 为 $6$ 米，斜面坡度为 $1$ ： $2$ ，则斜坡 $A B$ 的长为（）

A、 $4 \sqrt{3}$ 米 B、 $6 \sqrt{5}$ 米 C、 $12 \sqrt{5}$ 米 D、 $24$ 米

查看试题解析
9. 如图所示，利用标杆 $B E$ 测量建筑物的高度．已知标杆 $B E$ 高1.2m，测得 $A B =$ 1.6m， $B C =$ 12.4m. 则建筑物 $C D$ 的高是（）

A、9.3m B、10.5m C、12.4m D、14m

查看试题解析
10. 如图，平行于x轴的直线与函数y= $\frac{k_{1}}{x}$ （k₁>0，x>0），y= $\frac{k_{2}}{x}$ （k₂>0，x>0)的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k₁-k₂的值为（）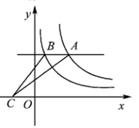

A、8 B、-8 C、4 D、-4

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 若 $\frac{x}{y} = \frac{2}{7}$ ，则 $\frac{x + y}{y} =$ .

查看试题解析
12. 已知关于 $x$ 的方程 $x^{2} + m x - 20 = 0$ 的一个根是 $- 4$ ，则它的另一个根是．

查看试题解析
13. 跳高训练时，甲、乙两名同学在相同条件下各跳了 $10$ 次，统计他们的平均成绩都是 $1.36$ 米，且方差为 $S_{甲}^{2} = 0.4$ ， $S_{乙}^{2} = 0.3$ ，则成绩较为稳定的是 $($ 填“甲”或“乙” $)$ ．

查看试题解析
14. 在 $△ A B C$ 中，若 $∠ A$ ， $∠ B$ 满足 $| c o s A - \frac{\sqrt{3}}{2} | + (1 - t a n B)^{2} = 0$ ，则 $∠ C =$ ．

查看试题解析
15. 已知：如图，在 $△ A B C$ 中，点 $E$ 在边 $A B$ 上，点 $F$ 在 $A C$ 边上，要使 $△ A F E$ ∽ $△ A B C$ ，则需要增加的一个条件是 $. ($ 写出一个即可 $)$

查看试题解析
16. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图，其对称轴 $x = - 1$ ，给出下列结果： $① b^{2} > 4 a c$ ； $② a b c > 0$ ； $③ 2 a + b = 0$ ； $④ a - b + c < 0$ ； $⑤ 3 a + c > 0 .$ 其中正确结论的序号是．

查看试题解析

三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。

17. 计算： $\sqrt{16} - 2 t a n 45 ° + | - 3 | + (π - 2023)^{0}$ ．

查看试题解析
18. 如图， $△ A B C$ 三个顶点坐标分别为 $A (- 1，3)$ ， $B (- 1，1)$ ， $C (- 3，2)$ ．

(1)、请画出 $△ A B C$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、以原点 $O$ 为位似中心，将 $△ A_{1} B_{1} C_{1}$ 放大为原来的 $2$ 倍．

查看试题解析
19. 如图所示，一次函数 $y_{1} = - x + m$ 与反比例函数 $y_{2} = \frac{k}{x}$ 相交于点 $A$ 和点 $B (3 ， - 1)$ ．

(1)、求 $m$ 的值和反比例函数解析式；

(2)、当 $y_{1} > y_{2}$ 时，求 $x$ 的取值范围．

查看试题解析
20. 某区教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名个学生进行科学知识测试，按照测试成绩分优秀，良好、合格与不合格四个等级，并绘制了如图所示两幅不完整统计图．

(1)、参与本次测试的学生人数为， $m =$ ；

(2)、请补全条形统计图；

(3)、若全区该年级共有 $5000$ 名学生，请估计该年级对科学知识掌握情况较好 $($ 测试成绩能达到良好及以上等级 $)$ 的学生人数．

查看试题解析
21. 某运动服专卖店在销售中发现，某款运动服每件进价为 $80$ 元，销售价为 $120$ 元时，每天可售出 $20$ 件，为了迎接国庆节，该店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件运动服降价 $1$ 元，那么平均可多售出 $2$ 件．

(1)、设每件童装降价元时，每天卖出件，每件可盈利元； $($ 用 $x$ 的代数式表示 $)$

(2)、若该专卖店计划平均每天盈利 $1200$ 元，那么每件运动服应降价多少元？

查看试题解析
22. 如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F．

(1)、求证：△ABE∽△DFA；

(2)、若AB＝6，BC＝4，求DF的长．

查看试题解析
23. 某次军事演习中，一艘船以 $40 k m / h$ 的速度向正东航行，在出发地 $A$ 测得小岛 $C$ 在它的北偏东 $60 °$ 方向， $2$ 小时后到达 $B$ 处，测得小岛 $C$ 在它的北偏西 $45 °$ 方向，求该船在航行过程中与小岛 $C$ 的最近距离（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ．结果精确到 $0.1 k m$ ）．

查看试题解析
24. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号，他们将其中某些材料摘录如下：对于三个实数 $a$ ， $b$ ， $c$ ，用 $M {a ， b ， c}$ 表示这三个数的平均数，用 $m i n {a ， b ， c}$ 表示这三个数中最小的数，例如： $M {1，2 ， 9} = \frac{1 + 2 + 9}{3} = 4 ， m i n {1，2 ， - 3} = - 3$ ．
请结合上述材料，解决下列问题：

(1)、 $M {2^{2} ， \sqrt{9} ， - 3^{2}} =$ ；

(2)、若 $M {- 2 x ， x^{2} ， 3} = 2$ ，求 $x$ 的值；

(3)、若 $a > 0$ ，且点 $P (M {- 2 ， a - 1，2 a}$ ， $m i n {- 2 ， a - 1，2 a})$ 在反比例函数 $y = \frac{- 2}{x}$ 的图象上，求 $a$ 的值．

查看试题解析
25. 如图，已知抛物线过点 $O (0，0)$ ， $A (5，5)$ ，且它的对称轴为 $x = 2$ ．

(1)、求此抛物线的解析式；

(2)、若点 $B$ 是抛物线对称轴上的一点，且点 $B$ 在第一象限，当 $△ O A B$ 的面积为 $15$ 时，求 $B$ 的坐标；

(3)、 $P$ 是抛物线上的动点，当 $P A - P B$ 的值最大时，求 $P$ 的坐标以及 $P A - P B$ 的最大值．

查看试题解析