山东省青岛市李沧区2023-2024学年七年级上学期期中数学试题

试卷更新日期：2024-01-17 类型：期中考试

进入出卷网下载

一、单项选择题（本题共8小题，每小题3分，共24分．在每个题给出的四个选项中，只有一项是符合题目要求的）

1. 下面现象能说明“面动成体”的是（）

A、流星从空中划过留下的痕迹 B、扔一块小石子，小石子在空中飞行的路线 C、时钟秒针旋转时扫过的痕迹 D、将一枚硬币竖立在桌面，击打一侧使其快速旋转，就会看到一个“球”

查看试题解析
2. 如图是一个正方体盒子展开后的平面图形，六个面上分别写有“数”、“学”、“核”、“心”、“素”、“养”，则“素”字对面的字是（）

A、核 B、心 C、数 D、学

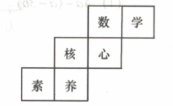查看试题解析
3. 在 $- 2^{2}$ ， ${(- 2)}^{2}$ ， $- (- 2)$ ， $- | - 2 |$ 中，负数的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 2023年9月23日，伴随着主火炬台上的熊熊火焰，第19届亚洲运动会在杭州盛大开幕．本次开幕式主火炬的燃料——零碳甲醇，燃烧高效、排放清洁，在人类历史上第一次被用于大型体育赛事．此次点燃的主火炬塔在大火状态下，燃烧1小时仅需 $550000 g$ 燃料．将数据550000用科学记数法表示为（）

A、 $5.5 \times 1 0^{5}$ B、 $55 \times 1 0^{4}$ C、 $0.55 \times 1 0^{6}$ D、 $5.5 \times 1 0^{6}$

查看试题解析
5. 下列几何体中，从正面和左面看到的形状图相同的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列运算正确的是（）

A、 $- 3^{2} = 9$ B、 ${(- 4)}^{3} = - 12$ C、 $- \frac{2^{2}}{3} = \frac{4}{3}$ D、 $- {(- \frac{1}{2})}^{3} = \frac{1}{8}$

查看试题解析
7. 已知 $| a | = 4$ ， b是3的相反数，则 $a + b$ 的值为（）

A、－7 B、－1 C、－7或1 D、1或－1

查看试题解析
8. 如图，用总长度为12米的木料，做成一个窗框．如果窗框横档的长度为x米，那么窗框的面积是（）

A、 $x (6 - x)$ 平方米 B、 $x (6 - \frac{3}{2} x)$ 平方米 C、 $x (6 - 3 x)$ 平方米 D、 $x (12 - x)$ 平方米

查看试题解析

二、多项选择题（本题共2小题，每小题4分，共8分．每小题的四个选项中，有多项符合题目要求，全部选对得4分，部分选对得2分，有错选得0分）

9. 下列说法正确的有（）

A、 $- 2 a^{2} b$ 与 $5 a b^{2}$ 是同类项 B、单项式 $2^{2} x^{3} y^{2}$ 的次数是5 C、多项式 $3 a b^{3} - 5 a^{2} + 1$ 的次数是4 D、单项式 $- \frac{π}{16} x^{3} y^{2}$ 的系数是 $- \frac{1}{16}$

查看试题解析
10. 在古埃及纸草书中，人们把分子为1的分数叫做埃及分数，一个埃及分数能写成两个不相等的埃及分数的和，即 $\frac{1}{n} = \frac{1}{n + 1} + \frac{1}{n (n + 1)}$ ．根据这个规律，下列式子正确的有（）

A、 $\frac{1}{9} = \frac{1}{10} + \frac{1}{90}$ B、 $\frac{1}{n (n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$ C、 $\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} = \frac{1}{3}$ D、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \cdot \cdot \cdot + \frac{1}{99 \times 100} = \frac{49}{100}$

查看试题解析

三、填空题（本大题共6小题，每小题3分，共18分）

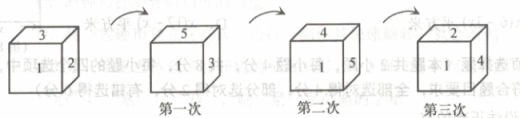
11. 中国是最早采用正负数表示相反意义量的国家，如果盈利100元记作＋100元，那么亏损10元可记作元．

查看试题解析
12. 比较大小： $- \frac{5}{6}$ －2.7（填“ $>$ ”，“ $<$ ”或“ $=$ ”）．

查看试题解析
13. 在圆柱、圆锥、长方体这三种几何体中，截面不可能是长方形的是．

查看试题解析
14. 已知一个直棱柱共有15条棱，它的底面边长都是5cm，侧棱长都是4cm，则这个棱柱的所有侧面的面积之和是 $c m^{2}$ ．

查看试题解析
15. 某学校计划购买甲、乙两种品牌的电子白板共30台．甲、乙两种品牌电子白板的单价分别为2.5万元/台和1.5万元/台．若购买甲品牌电子白板的总费用为 $2.5 (18 + n)$ 万元，则购买乙品牌电子白板的总费用为万元（用含n的代数式表示）．

查看试题解析
16. 一个小正方体的六个面分别标有数字1，2，3，4，5，6．将它按如图所示的方式顺时针滚动，每滚动90°算一次，则滚动第2023次时，小正方体朝下一面标有的数字是．

查看试题解析

四、解答题（本题共9道小题，满分70分）

17. 一个几何体由若干个棱长为1的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数．

(1)、请画出从正面看到的这个几何体的形状图；

(2)、若给这个几何体喷上颜色（底面不喷色），则需要喷色的面积为．

查看试题解析
18. 计算

(1)、 $25 + (- 15)$ ；

(2)、 $(- 3.1) - (- 4.5)$ ；

(3)、 $(- \frac{5}{6} + \frac{3}{8}) \times (- 24)$ ；

(4)、 $2 \times {(- \frac{1}{4})}^{2} - (- 12) \div (- 3)$ ．

查看试题解析
19. 化简下列各式

(1)、 $4 a - (a - 3 b)$ ；

(2)、 $- 3 (2 x^{2} - x y) + 4 (x^{2} + x y)$

查看试题解析
20. 求代数式的值
已知 $A = x^{2} + x y - 2 y$ ， $B = 2 x^{2} + 2 x y + x - 1$ ．当 $x = - 2$ ， $y = \frac{1}{4}$ 时，求代数式 $2 A - B$ 的值．

查看试题解析
21. 为丰富校园体育生活，某校增设网球兴趣小组，需要采购某品牌网球训练拍30支，网球x筒 $(x > 30)$ ，现从甲、乙两家商店了解到该品牌网球拍每支定价均为80元，网球每筒均为20元，并且多买都有一定的优惠．甲商店的优惠条件是：买一支网球拍送一筒网球；乙商店的优惠条件是：网球拍与网球均按九折付款．

(1)、选择甲商店购买，所需的费用为元；选择乙商店购买，所需的费用为元（用含x的代数式表示）；

(2)、当购买网球的数量为100筒时，请通过计算说明选择哪家商店所需费用较少．

查看试题解析
22. 为保障校园体育活动安全有序的开展，学校计划在足球场四周安装防护栏．如图，每根立柱的直径为0.08米，相邻两根立柱之间设置一张防护网，每张防护网长3米．

(1)、根据上述信息，完成下表：
立柱根数
2
3
4
5
…
n
防护栏长度（米）
3.16
6.24

12.4
…

(2)、当防护栏总长度为74米时，求立柱的根数，

查看试题解析
23. 我们知道， $4 x - 3 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ． “整体思想”是一种重要的数学思想方法，它在多项式的化简与求值中应用极为广泛．

(1)、把 ${(m - n)}^{2}$ 看成一个整体，合并 $2 {(m - n)}^{2} - 7 {(m - n)}^{2} + 3 {(m - n)}^{2}$ 的结果是．

(2)、已知 $x^{2} - 2 y = 4$ ，则 $4 x^{2} - 8 y - 10$ 的值为．

(3)、已知 $a - 2 b = - 5$ ， $2 b - c = 2$ ， $c - d = 12$ ，则 $(a - c) + (2 b - d) - (2 b - c)$ 的值为．

查看试题解析
24. “电商平台＋消费扶贫”新模式，拓宽了农产品销售渠道．某农户在网上销售木耳，原计划每天卖100斤，下表统计的是某周的销售情况（超额记为正，不足记为负，单位：斤）
星期
一
二
三
四
五
六
日
与计划量的差值
－3
－3
＋1
＋4
－8
＋10
＋12

(1)、销售量最多的一天比销售量最少的一天多销售斤；

(2)、该周实际销售总量（填“大于”“等于”或“小于”）计划销售总量；

(3)、若每斤按50元出售，则该周共收入多少元?

查看试题解析
25. 【阅读材料】
数轴是一种非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与形之间的联系．
两个有理数在数轴上对应的点之间的距离，可以用这两个数的差的绝对值表示．如图，在数轴上有理数a对应的点为A ，有理数b对应的点为B ，则A ， B两点之间的距离可表示为 $| a - b |$ 或 $| b - a |$ ，记为 $| A B | = | a - b | = | b - a |$ ．

(1)、【解决问题】
数轴上有理数－6与1对应的两点之间的距离是；

(2)、数轴上有理数m与－4对应的两点之间的距离是（用含m的式子表示）；

(3)、若数轴上有理数n与－1对应的两点之间的距离是5，则 $n =$ ．

(4)、【拓展应用】点M，N，P是数轴上的三个点，其中，点M表示的数为2，点N表示的数为－3，
点P表示的数为x．
若点P在点M ， N之间，则 $| x + 3 | + | x - 2 | =$ ；若 $| x + 3 | + | x - 2 | = 10$ ，则 $x =$ ．

查看试题解析

星期	一	二	三	四	五	六	日
与计划量的差值	－3	－3	＋1	＋4	－8	＋10	＋12

立柱根数	2	3	4	5	…	n
防护栏长度（米）	3.16	6.24		12.4	…