江西省九江市修水县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2024-01-17 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
-
1. 下列关于x的方程中,一定是一元二次方程的为( )A、 B、 C、 D、2. 下列说法中错误的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形3. 如图,在中,点在边上,过点作 , 交于点 . 若 , , 则的值是( )
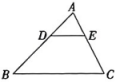 A、 B、 C、 D、4. 某校举办文艺会演,在主持人选拔环节中,有一名男同学和三名女同学表现优异.若从以上四名同学中随机抽取两名同学担任主持人,则刚好抽中一名男同学和一名女同学的概率是( )A、 B、 C、 D、5. 如图,四边形是正方形,延长到点 , 使 , 则的度数是( )
A、 B、 C、 D、4. 某校举办文艺会演,在主持人选拔环节中,有一名男同学和三名女同学表现优异.若从以上四名同学中随机抽取两名同学担任主持人,则刚好抽中一名男同学和一名女同学的概率是( )A、 B、 C、 D、5. 如图,四边形是正方形,延长到点 , 使 , 则的度数是( )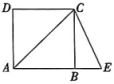 A、 B、 C、 D、6. 两千多年前,我国学者墨子和他的学生做了小孔成像的实验.他们的做法是:在一间黑暗屋子里的一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小宇在学习了小孔成像的原理后,利用如图所示装置来观察小孔成像的现象.已知一根点燃的蜡烛距小孔(P)20cm,光屏在距小孔30cm处,小宇测得蜡烛的火焰高度为4cm,则光屏上火焰所成像的高度为( )
A、 B、 C、 D、6. 两千多年前,我国学者墨子和他的学生做了小孔成像的实验.他们的做法是:在一间黑暗屋子里的一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小宇在学习了小孔成像的原理后,利用如图所示装置来观察小孔成像的现象.已知一根点燃的蜡烛距小孔(P)20cm,光屏在距小孔30cm处,小宇测得蜡烛的火焰高度为4cm,则光屏上火焰所成像的高度为( )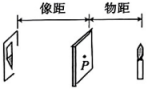 A、8cm B、6cm C、5cm D、4cm
A、8cm B、6cm C、5cm D、4cm二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 一元二次方程配方后得 , 则的值是 .8. 已知 , 若 , 则 .9. 一个不透明的布袋中装有红色、蓝色、白色球共60个,这些球除颜色外其他完全相同.小明通过多次摸球试验后发现,摸到红色球的频率稳定在 , 则布袋中红色球可能有个.10. 如图,和是以点为位似中心的位似图形,相似比为: , 则和的面积比是 .
 11. 已知关于x的一元二次方程的两个实数根分别为 , 则的值为 .12. 在菱形中, , 点在上, . 若点是菱形四条边上异于点的一点, , 则的长为 .
11. 已知关于x的一元二次方程的两个实数根分别为 , 则的值为 .12. 在菱形中, , 点在上, . 若点是菱形四条边上异于点的一点, , 则的长为 .三、(本大题共5小题,每小题6分,共30分)
-
13. 解方程:(1)、;(2)、 .14. 已知关于x的方程 , 当该方程的一个根为时,求m的值及方程的另一个根.15. 为了落实“双减”政策,弘扬非遗(非物质文化遗产)传统文化,某校拟组织课外兴趣班的同学参观以下项目:A(修水陶艺),B(修水采茶戏),C(九江山歌),D(德安潘公戏).小明和小涵随机报名参观其中一项.(1)、“小明参观九江山歌”这一事件是;(请将正确答案的序号填写在横线上)
①必然事件;②不可能事件;③随机事件.
(2)、请用列表或画树状图的方法,求小明和小涵参观的项目都是修水的非物质文化遗产的概率.16. 如图,在矩形中,分别是的中点,请仅用无刻度的直尺按下列要求作图. 图1
图1 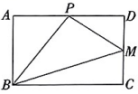 图2(1)、在图1中,作出的边上的中线;(2)、在图2中,以为边作一个菱形.17. 台风“杜苏芮”牵动着全国人民的心.某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款3000元,第三天收到捐款4320元.(1)、如果第二天、第三天收到的捐款的增长率相同,求捐款的增长率.(2)、按照(1)中收到的捐款的增长速度,第四天该单位能收到多少捐款?
图2(1)、在图1中,作出的边上的中线;(2)、在图2中,以为边作一个菱形.17. 台风“杜苏芮”牵动着全国人民的心.某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款3000元,第三天收到捐款4320元.(1)、如果第二天、第三天收到的捐款的增长率相同,求捐款的增长率.(2)、按照(1)中收到的捐款的增长速度,第四天该单位能收到多少捐款?四、(本大题共3小题,每小题8分,共24分)
-
18. 如图, , 交于点 , 且 .
 (1)、求的长.(2)、求证: .19. 如图,在中, , 为的中线, , , 连接 .
(1)、求的长.(2)、求证: .19. 如图,在中, , 为的中线, , , 连接 .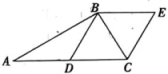 (1)、求证:四边形为菱形.(2)、连接 , 若 , , 求的长.20. 如图,在中, , 为的中点,四边形是平行四边形,相交于点 .
(1)、求证:四边形为菱形.(2)、连接 , 若 , , 求的长.20. 如图,在中, , 为的中点,四边形是平行四边形,相交于点 .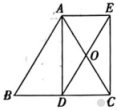 (1)、求证:四边形是矩形.(2)、若 , , 求的长.
(1)、求证:四边形是矩形.(2)、若 , , 求的长.五、(本大题共2小题,每小题9分,共18分)
-
21. 已知关于x的方程 .(1)、求证:无论取何实数值,方程总有实数根.(2)、若等腰三角形的一边长 , 另两边长恰好是这个方程的两个根,求的周长.22. 如图, , , 是边上一点,且 .
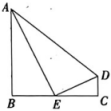 (1)、求证: .(2)、若 , 求的长.(3)、当时,请写出线段之间的数量关系,并说明理由.
(1)、求证: .(2)、若 , 求的长.(3)、当时,请写出线段之间的数量关系,并说明理由.六、(本大题共12分)
-
23. 将正方形与正方形按图1所示方式放置,点在同一条直线上,点在边上, , 连接 .
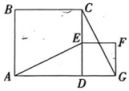 图1
图1 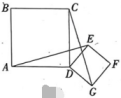 图2(1)、线段的关系为 .(2)、将正方形绕点顺时针旋转一个锐角后,如图2,(1)中的结论是否仍然成立?请说明理由.(3)、在正方形绕点顺时针旋转一周的过程中,是否存在的时刻?若存在,请直接写出此时AE的长;若不存在,请说明理由.
图2(1)、线段的关系为 .(2)、将正方形绕点顺时针旋转一个锐角后,如图2,(1)中的结论是否仍然成立?请说明理由.(3)、在正方形绕点顺时针旋转一周的过程中,是否存在的时刻?若存在,请直接写出此时AE的长;若不存在,请说明理由.