湖南省湖湘C13教育联盟2023-2024学年九年级上学期数学月考考试试卷（12月）

试卷更新日期：2024-01-17 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 若 $c o s α = 0.5$ ，则 $α$ 的度数为（）

A、60° B、45° C、30° D、90°

查看试题解析
2. 一元二次方程 $x^{2} = 10 x$ 的根是（）

A、 $x = 10$ B、 $x_{1} = 0$ ， $x_{2} = 10$ C、 $x = - 10$ D、 $x_{1} = 0$ ， $x_{2} = - 10$

查看试题解析
3. 反比例函数 $y = \frac{1 - k}{x}$ 的图象在每一个象限内 $y$ 随 $x$ 值的增大而增大，则 $k$ 的取值范围是（）

A、 $k > \frac{1}{2}$ B、 $k > 1$ C、 $k < \frac{1}{2}$ D、 $k < 1$

查看试题解析
4. 若点 $A (1 ， \sqrt{2 n - 4})$ 在第一象限，则 $n$ 的取值范围是（）

A、 $n < 2$ B、 $n \leq 2$ C、 $n > 2$ D、 $n \geq 2$

查看试题解析
5. 已知方程 $x^{2} - 6 x + n = 0$ 可以配方成 ${(x - m)}^{2} = 7$ ，则 ${(m - n)}^{2023}$ 的值为（）

A、0 B、1 C、-1 D、 $2^{2023}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ，若 $A E ： E C = 1 ： 2$ ，则下列结论中正确的是（）

A、 $\frac{D E}{B C} = \frac{1}{2}$ B、 $\frac{△ A D E 的周长}{△ A B C 的周长} = \frac{1}{2}$ C、 $\frac{△ A D E 的面积}{△ A B C 的面积} = \frac{1}{4}$ D、 $\frac{△ A D E 的周长}{△ A B C 的周长} = \frac{1}{3}$

查看试题解析
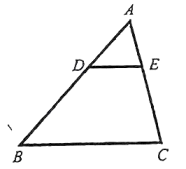7. 在 $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ，把 $∠ A$ 的邻边 $b$ 与对边 $a$ 的比叫做 $∠ A$ 的余切，记作 $c o t A = \frac{b}{a}$ .则下列关系式中不成立的是（）

A、 $c o t 3 0^{∘} = 1$ B、 $c o t 4 5^{∘} = 1$ C、 $t a n A \cdot c o t A = 1$ D、 $t a n A = c o t (9 0^{∘} - A)$

查看试题解析
8. 若函数 $y = \frac{\sqrt{k - 1}}{x}$ 是反比例函数，则一元二次方程 $k x^{2} + 4 x + 4 = 0$ 的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、有一个实数根 D、没有实数根

查看试题解析
9. 如图，以 $△ A B C$ 三边为边向外作正方形，面积分别是 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，若 $S_{1} + S_{2} = S_{3}$ ，且 $S_{1} = 9$ ， $S_{2} = 16$ ，则 $s i n A$ 等于（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
10. 如图，在 $R t △ A M N$ 与矩形 $A B C D$ 中，一直角边 $A N$ 经过点 $C$ ，另一直角边 $A M$ 与 $C B$ 的延长线交于点 $E$ ，与 $D B$ 的延长线交于点 $F$ ，则下列结论错误的是（）

A、 $△ A E B ∽ △ C A B$ B、 $△ A F B ∽ △ B F E$ C、 $\frac{A E}{A C} = \frac{B F}{A F}$ D、 $\frac{A E}{E C} = \frac{B F}{A F}$

查看试题解析

二、填空题（每小题3分，共18分）

11. 计算： $\sqrt{\frac{2}{5}} \times \sqrt{10} =$ .

查看试题解析
12. 在 $△ A B C$ 中， $∠ C = 9 0^{∘}$ ， $c o s A = \frac{\sqrt{2}}{2}$ ， $B C = 10$ ，则 $A B =$ .

查看试题解析
13. 劳动实践课上，小明提着一桶水，沿一斜坡向上走了50米，若斜坡坡比是 $1 ： \sqrt{3}$ ，则小明提水上升的高度是米.

查看试题解析
14. 已知t是方程 $x^{2} - 2 x - 3 = 0$ 的一个根，则 $t - \frac{3}{t} =$ .

查看试题解析
15. 在平面直角坐标系中，函数 $y = \frac{2}{x} (x > 0)$ 与 $y = x - 1$ 的图象交于点 $P (a ， b)$ ，则代数式 $a - b + a b$ 的值为.

查看试题解析
16. 如图，平面直角坐标系中，点 $A$ 是 $x$ 轴上任意一点， $B C$ 平行于 $x$ 轴，分别交 $y = - \frac{2}{x} (x < 0)$ ， $y = \frac{k}{x} (x > 0)$ 的图象于 $B$ ， $C$ 两点，若 $△ A B C$ 的面积为3，则、 $k$ 值为.

查看试题解析

三、解答题（共72分）

17. 计算 $2 t a n 6 0^{∘} - {(2023 - π)}^{0} - \sqrt{12} + {(\frac{1}{2})}^{- 1}$ .

查看试题解析
18. 已知在直角坐标平面内， $△ A B C$ 三个顶点的坐标分别为 $A (2 ， 0)$ ， $B (3 ， 2)$ ， $C (- 1 ， 1)$ .（网格中每个小正方形的边长是一个单位长度）

(1)、以点 $O$ 为位似中心，在网格内画出 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 位似，且位似比为 $2 ： 1$ ；

(2)、线段 $B_{1} C_{1}$ 的长度是.

查看试题解析
19. 如图，已知 $△ A B C$ 中，点 $D$ 是边 $A B$ 上一点，点 $E$ 是 $△ A B C$ 外一点， $∠ A C D = ∠ B C E$ ， $∠ A = ∠ C D E$ .

(1)、求证： $△ C D E ∽ △ C A B$ ；

(2)、若 $C D = C B = 5$ ，求 $A C \cdot E C$ 的值.

查看试题解析
20. 已知 $▱ A B C D$ 的两对角线 $A C$ ， $B D$ 的长是关于 $x$ 的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 的两个实数根.

(1)、若 $A C$ 的长为1，求 $m$ 的值；

(2)、当 $m$ 为何值时， $▱ A B C D$ 是矩形.

查看试题解析
21. 随着新能源汽车技术的提高，电能源汽车正逐渐成为人们喜爱的交通工具.某4S店新能源汽车销售量自2023年起逐月增加，据统计，该4S店1月份销售新能源汽车32辆，3月份销售了50辆.

(1)、求该4S店这两个月的月平均增长率；

(2)、若月平均增长率保持不变，求该4S店4月份卖出多少辆新能源汽车.（答案若含有小数则只取整数部分，不四舍五人）

查看试题解析
22. 如图， $△ A B C$ 中， $∠ C A B = 6 0^{∘}$ ， $∠ A B C = 4 5^{∘}$ ，点 $A$ ， $B$ 在 $x$ 轴上，反比例函数 $y = \frac{k}{x}$ 的图象经过点 $C (1 ， 2 \sqrt{3})$ ，且与 $B C$ 边交于另一点 $D$ ， $C E ⊥ x$ 轴，垂足为点 $E$ .

(1)、求反比例函数的解析式；

(2)、求点 $D$ 的坐标；

(3)、在 $x$ 轴上是否存在点 $P$ ，使得 $△ B D P$ 与 $△ B C E$ 相似，若存在，请直接写出满足条件点 $P$ 的坐标，若不存在，请说明理由.

查看试题解析
23. 如图，一学生站在 $A$ 处，利用无人机测量大楼 $B C$ 的高度，无人机在空中点 $P$ 处，测得点 $P$ 与地面上 $A$ 点， $B$ 点处俯角分别为 $∠ M P A$ 和 $∠ N P B$ ，且 $t a n ∠ M P A = \frac{4}{3}$ ， $t a n ∠ N P B = 4$ ， $A B = 80 m$ .（点 $A$ ， $B$ ， $C$ ， $P$ 在同一平面内）

(1)、求无人机 $P$ 到地面的距离；

(2)、若 $∠ B C P = 12 0^{∘}$ ，求大楼 $B C$ 的高度.（结果精确到 $0.1 m$ ）
（参考数据： $\sqrt{3} \approx 1.73$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
24. 【引入命题】设 $A (x)$ 是关于字母 $x$ 的一个整式，若 $x_{1}$ 是方程 $A (x) = 0$ 的一个根，则整式 $A (x)$ 必有一个因式 $(x - x_{1})$ ，即 $A (x) = (x - x_{1}) A_{1} (x)$ .其中 $A_{1} (x)$ 仍然是关于字母 $x$ 的一个整式.

(1)、若 $A (x) = (x - 2) A_{1} (x)$ ，则 $A (x) = 0$ 的一个根是；

(2)、【回归课本】设一元二次方程 $a x^{2} + b x + c = 0$ 有两个根 $x_{1}$ ， $x_{2}$ ，则方程可化为： $a (x - x_{1}) (x - x_{2}) = 0$ ，即 $a x^{2} - a (x_{1} + x_{2}) x + a x_{1} x_{2} = 0$ ，与原方程比较系数，可得到一元二次方程根与系数的关系： $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ .
利用上式结论解题：已知关于 $x$ 的一元二次方程 $x^{2} + 2 m x + m^{2} - m + 2 = 0$ 有两个不相等的实数根，且 $x_{1} + x_{2} + x_{1} x_{2} = 2$ ，求实数 $m$ 的值；

(3)、【探究引申】设一元三次方程 $a x^{3} + b x^{2} + c x + d = 0$ 有三个根 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，则原方程可化为： $a (x - x_{1}) (x - x_{2}) (x - x_{3}) = 0$ ，试着展开上式，然后比较系数，可以得到根与系数的关系： $x_{1} + x_{2} + x_{3} = - \frac{b}{a}$ ， $x_{1} x_{2} + x_{2} x_{3} + x_{1} x_{3} = \frac{c}{a}$ ， $x_{1} \cdot x_{2} \cdot x_{3} = - \frac{d}{a}$ .
利用上式结论解题：已知方程 $x^{3} - 4 x^{2} + 3 x + d = 0$ 有三个根 $α$ ， $β$ ， $γ$ ，求 $α^{2} + β^{2} + γ^{2}$ 的值；

(4)、【拓展提高】利用以上规律探究：若方程 $a_{0} x^{n} + a_{1} x^{n - 1} + ⋯ + a_{n - 1} x + a_{n} = 0 (a_{0} \neq 0)$ 有 $n$ 个根 $x_{1}$ ， $x_{2}$ ， …， $x_{n}$ ，则 $x_{1} + x_{2} + ⋯ + x_{n} =$ ， $x_{1} \cdot x_{2} \cdot ⋯ \cdot x_{n} =$ .

查看试题解析
25. 定义：如图1，线段 $A B$ 与线段 $C D$ 交于点 $P$ ，若 $△ P A D ∽ △ P C B$ ，则我们称此图形为“蝴蝶结”形.

(1)、若图1是“蝴蝶结”形，连接 $A C$ 与 $B D$ （如图2），试说明 $△ P A C$ 与 $△ P D B$ 组成的图形也是“蝴蝶结”形；（此时，我们称四边形 $A C B D$ 为“双蝴蝶结”四边形）

(2)、如图3，在“双蝴蝶结”四边形 $A C B D$ 中，点 $E$ 在边 $B D$ 上，连接 $P E$ ，若 $A C = B C$ ， $∠ P E B = 2 ∠ C A B$ ，求证： $\frac{D E}{A D} + \frac{P E}{B D} = 1$ ；

(3)、如图2，若“双蝴蝶结”四边形 $A C B D$ ， $△ P A C$ ， $△ P B D$ 的面积依次为 $S$ ， $S_{1}$ ， $S_{2}$ ，且 $\sqrt{S} = \sqrt{S_{1}} + \sqrt{S_{2}}$ ，试判断 $△ P A C$ ， $△ P B D$ 的形状，并说明理由.

查看试题解析