安徽省芜湖市无为市多校联考2023-2024学年九年级上学期月考数学试题

试卷更新日期：2024-01-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的．

1. 下列图标中，是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 下列诗句所描述的事件中是必然事件的是（）．

A、千山鸟飞绝 B、手可摘星辰 C、黄河入海流 D、大漠孤烟直

查看试题解析
3. 在平面直角坐标系中，以原点O为圆心，2为半径作 $⊙ O$ ，点M的坐标是 $(1 ， 1)$ ，则点M与 $⊙ O$ 的位置关系是（）．

A、点M在圆内 B、点M在圆外 C、点M在圆上 D、无法确定

查看试题解析
4. 如图，在一个圆形转盘中，标有黄、红、绿的三个扇形的圆心角度数分别为 $60 °$ 、 $90 °$ 、 $210 °$ ．让转盘自由转动，转盘停止后指针（若指针落在分界线上，则重新转动转盘）落在红扇形的概率是（）．

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{7}{12}$

查看试题解析
5. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，若 $⊙ O$ 的边心距 $d = \sqrt{6}$ ，则正六边形的边长是（）．

A、 $2 \sqrt{2}$ B、3 C、6 D、 $2 \sqrt{3}$

查看试题解析
6. 某校“研学”活动小组在一次户外实践时，发现一种植物的1个主干上长出x个枝干，每个枝干上再长出x个小分支．若在一个主干上的主干、枝干和小分支的数量之和是57个，则根据题意，下列方程正确的是（）．

A、 $1 + x^{2} = 57$ B、 ${(1 + x)}^{2} = 57$ C、 $x + x^{2} = 57$ D、 $1 + x + x^{2} = 57$

查看试题解析
7. 已知 $⊙ O$ 的半径是一元二次方程 $x^{2} - 4 x + 4 = 0$ 的解，且点O到直线AB的距离为2，则 $⊙ O$ 与直线AB的位置关系为（）．

A、相交 B、相切 C、相离 D、无法确定

查看试题解析
8. 如图，有两副手套（区分左、右手）共四只，除颜色外其余均相同，将它们放置于桌面上，分别用 $P_{1}$ ， $P_{2}$ ， $Q_{1}$ ， $Q_{2}$ 表示，小明先从两只左手手套随机取一只，再从两只右手手套中随机取一只，则恰好匹配成一双相同颜色的手套的概率是（）．

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{6}$

查看试题解析
9. 如图，边长为3的正方形 $A B C D$ 的中心与半径为1的 $⊙ O$ 的圆心重合，过点O作 $O E ⊥ O F$ ，分别交AB ， AD于点E ， F ，则阴影部分的面积是（）．

A、 $9 - \frac{π}{4}$ B、 $\frac{9}{4} - \frac{π}{2}$ C、 $\frac{9}{4} - \frac{π}{4}$ D、随点E ， F的位置而变化

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ （a ， b ， c为常数， $a > 0$ ）的顶点坐标为 $(2 ， - 3)$ ，与x轴的两个交点分别为 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ，且 $4 < x_{2} < 6$ ，有以下3个结论：① $b^{2} - 4 a c > 0$ ；② $- 2 < x_{1} < 0$ ；③ $4 a - 3 = c$ ．则正确的结论有（）．

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

11. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ C = 70 °$ ，将 $△ A B C$ 绕点B逆时针旋转得到 $△ D B E$ ，旋转角为 $α (α < 90 °)$ ，当点C的对应点E落在 $△ A B C$ 的边AC上时，旋转角 $α$ 的度数为．

查看试题解析
12. 若从甲、乙、丙3位老师中随机抽取1位担任“双减”政策宣讲志愿者，则抽到甲的概率是．

查看试题解析
13. 在平面直角坐标系中，已知 $⊙ P$ 的半径为2，圆心P在抛物线 $y = \frac{1}{2} x^{2} - 2$ 上运动，当 $⊙ P$ 与x轴相切，且圆心P在第二象限内时，圆心P的坐标为．

查看试题解析
14. 如图，AB与 $⊙ O$ 相切于点P ， AC ， BD均为 $⊙ O$ 的切线， $∠ A = 60 °$ ， $∠ A B D = 90 °$ ， $A C = 6$ ．

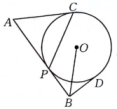(1)、PC的长为．

(2)、OB的长为．

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 解方程： $x^{2} - x - 2 = 0$

查看试题解析
16. 龙舞腾盛世，某学校为传承中华传统龙狮文化，开办了龙狮特色基地．如图，在训练中，龙的尾部由四名同学摆成了一个弧形，这弧形的弧长部分占龙总长的二分之一，已知弧形的半径为2米，圆心角为 $135 °$ ，求整条龙的长．

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 如图，正八边形 $A B C D E F G H$ 内接于 $⊙ O$ ， M是弧DE上的一点，连接AM ， BM ，求 $∠ A M B$ 的度数．

查看试题解析
18. 某校组织九年级学生参加安徽省地名知识竞赛．甲、乙、丙、丁四名同学在竞赛中综合得分相同，该校决定从这四名学生中随机选取两名学生参加区级竞赛．

(1)、事件“戊同学被选到”是事件．（填“随机”、“必然”或“不可能”）

(2)、请用列表或画树状图的方法，求恰好选到甲、乙两名同学的概率．

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 在一个不透明的口袋里，装有若干个除颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
78
123
b
402
644
801
摸到白球的频率 $\frac{m}{n}$
a
0.82
0.79
0.804
0.805
0.801

(1)、上表中的 $a =$ ， b= ．

(2)、“摸到白球”的概率的估计值是（精确到0.1）．

(3)、如果袋中有12个白球，那么袋中除了白球外，大约还有多少个其他颜色的小球？

查看试题解析
20. 如图，在等腰直角 $△ A B C$ 中，P是斜边BC上一点（不与点B ， C重合），PE是 $△ A B P$ 的外接圆 $⊙ O$ 的直径．

(1)、求 $∠ A P E$ 的度数．

(2)、若 $⊙ O$ 的直径为2，求 $P C^{2} + P B^{2}$ 的值．

查看试题解析

六、（本题满分12分）

21. 如图，AB为半圆O的直径，C是半圆O上一点，D是 $\overset{⌢}{A C}$ 的中点，过点D作直线 $l ∥ A C$ ， $A F ⊥$ 直线l ，垂足为F ， BC的延长线交直线l于点E ．

(1)、求证：直线l是 $⊙ O$ 的切线．

(2)、若 $⊙ O$ 的半径为1，求 $A F + B E$ 的值．

查看试题解析

七、（本题满分12分）

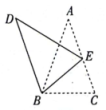
22. 如图，在 $R t △ A B C$ 中， $∠ A B C = 60 °$ ， D在斜边BC上，且为BC中点下方一动点，将边AD绕点A顺时针旋转 $60 °$ 得到AE ，连接DE ， EB ，延长AD ， EB交于点F ，连接CF ．

图1 图2

(1)、如图1， $∠ A B E =$ °；若 $A B = 2$ ，则点C到EB所在直线的距离为．

(2)、如图2，当 $D E ⊥ A B$ 时．
①直接写出AB与DE之间的数量关系；

查看试题解析

八、（本题满分14分）

23. 在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点．

(1)、求该抛物线的解析式，并写出它的对称轴．

(2)、 $P (x ， y)$ 是抛物线 $y = a x^{2} + b x + 3$ 上一动点，点 $P^{'}$ 与点P关于直线 $y = 1$ 对称，函数 $y^{'}$ 与自变量x的部分对应值如下表：
x
…
$- 1$
0
1
2
3
…
$y^{'}$
…
p
$- 1$
q
$- 1$
2
…
请直接写出p ， q的值，并在如图所示的平面直角坐标系中用平滑的曲线依次连接表中各点得到 $y^{'}$ 的图象．

(3)、若抛物线 $y = a x^{2} + b x + 3$ 关于直线 $y = m$ 对称的抛物线为L ，当 $- 2 \leq x \leq 2$ 时，抛物线L上最高点的纵坐标与最低点的纵坐标之和为15，请求出m的值．

查看试题解析

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	78	123	b	402	644	801
摸到白球的频率 $\frac{m}{n}$	a	0.82	0.79	0.804	0.805	0.801

x	…	$- 1$	0	1	2	3	…
$y^{'}$	…	p	$- 1$	q	$- 1$	2	…