安徽省芜湖市无为市多校联考2023-2024学年七年级上学期月考数学试题

试卷更新日期：2024-01-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是符合题目要求的.

1. 3的倒数是（）

A、3 B、 $- 3$ C、0.3 D、 $\frac{1}{3}$

查看试题解析
2. 若一元一次方程 $2 x - a = 3$ 的解是 $x = 1$ ，则a的值是（）

A、 $- 1$ B、1 C、 $- 5$ D、5

查看试题解析
3. ChatGPT是人工智能研究实验室OpenAI新推出的一种由人工智能技术驱动的自然语言处理工具，ChatGPT的背后离不开大模型、大数据、大算力，其技术底座有着多达1750亿个模型参数，数据1750亿用科学记数法表示为（）

A、 $1.75 \times 1 0^{3}$ B、 $1.75 \times 1 0^{11}$ C、 $1750 \times 1 0^{8}$ D、 $1.75 \times 1 0^{12}$

查看试题解析
4. 下列计算正确的是（）

A、 $a + b = a b$ B、 $2 a - a = 2$ C、 $2 a^{2} + a^{2} = 3 a^{4}$ D、 $- a^{2} b + 2 a^{2} b = a^{2} b$

查看试题解析
5. 等式就像平衡的天平，能与图中的事实具有相同性质的是（）

A、如果 $a = b$ ，那么 $a c = b c$ B、如果 $a = b$ ，那么 $a + c = b + c$ C、如果 $a = b$ ，那么 $\frac{a}{c} = \frac{b}{c} (c \neq 0)$ D、如果 $a = b$ ，那么 $a^{2} = b^{2}$

查看试题解析
6. 若单项式 $2 a^{x - 1} b^{4}$ 与单项式 $- 3 a^{3} b^{3 + y}$ 是同类项，则 $x + y$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
7. 若 $(a - 1) x^{{| a |}^{}} = 2$ 是关于的一元一次方程，则a的值为（）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
8. 如图，数轴上的点 $A$ 、 $B$ 、 $C$ 、 $D$ 分别对应有理数a、b、c、d，下列各式的值最小的是（）

A、 $| a |$ B、 $| b |$ C、 $| c |$ D、 $| d |$

查看试题解析
9. 随着网络及直播软件的普及，“直播带货”成为火热的营销模式之一.某运动品牌上衣在实体店按成本价提高30%销售，在直播间以实体客售价的9折进行销售，结果在直播间每卖出1件该上衣可获利34元，设该上衣的成本价为x元，根据题意可列方程（）

A、 $(1 + 30 % \cdot x) \cdot 0.9 = x + 34$ B、 $(1 + 30 % \cdot x) \cdot 0.9 = x - 34$ C、 $(1 + 30 %) x \cdot 0.9 = x + 34$ D、 $(1 + 30 %) x \cdot 0.9 = x - 34$

查看试题解析
10. 若关于的一元一次方程 $2023 x + m = x - 2023$ 的解为 $x = 6$ ，则关于 $y$ 的一元一次方程 $2023 (5 - y) - m = 2028 - y$ 的解为（）

A、 $y = - 11$ B、 $y = 2$ C、 $y = 10$ D、 $y = 11$

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

11. 计算 $2 + (- 4)$ 的结果是.

查看试题解析
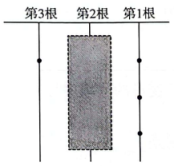
12. 单项式 $- 6 x^{4} y$ 的次数是.

查看试题解析
13. 我国古代《易经》一书中记载，远古时期人们通过在绳子上打结来记录数量，即“结绳计数”.如图，一位妇人在从右到左依次排列的绳子上打结，满五进一，用来记录采集到的野果的个数.她一共采集到了43个野果，则在第2根绳子上的打结数是个.

查看试题解析
14. 如图，点 $A$ 和点 $B$ 在数轴上，点 $A$ 在原点 $O$ 的左侧，点 $B$ 在原点 $O$ 的右侧，点 $B$ 表示的数是6，用 $O A$ 表示点 $O$ 与点 $A$ 之间的距离，用 $O B$ 表示点 $O$ 与点 $B$ 之间的距离，用 $A B$ 表示点 $A$ 和点 $B$ 之间的距离，且 $O A = 2 O B$ .动点 $P$ 从点 $B$ 出发以每秒4个单位长度的速度沿数轴负方向运动，同时动点 $Q$ 从原点 $O$ 出发以每秒1个单位长度的速度沿数轴负方向运动；当动点 $P$ 到达点 $A$ 时， $P$ ， $Q$ 两点同时停止运动.设点 $P$ 的运动时间为秒，用 $O P$ 表示点 $O$ 与点 $P$ 之间的距离，用 $O Q$ 表示点 $O$ 与点 $Q$ 之间的距离.

(1)、当点 $P$ 在点 $O$ 的右侧且 $O P = O Q$ 时， $t =$ .

(2)、当点 $P$ 在点 $O$ 的左侧且 $O P = \frac{4}{3} O Q$ 时， $t =$ .

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 计算： $(- 3 + 2) \times 4 + {(- 2)}^{3}$ .

查看试题解析
16. 解方程： $3 x + 4 = 14 - x$ .

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 先化简，再求值： $- a^{2} + 4 a + 1 + 3 (- 3 a + a^{2} - 2)$ ，其中a是最大的负整数.

查看试题解析
18. 课堂上，老师设计了“接力游戏”用合作的方式完成解方程，规则：一列同学每人只能看到前一人给的式子，并只完成解方程的一步变形，即前一个同学完成一步，后一个同学接着前一个同学的步骤进行下一步变形，直至解出方程.请根据下面的“接力游戏”回答问题.
接力游戏
老师： $\frac{3 x + 1}{4} - 1 = \frac{5 x - 4}{3}$ .
甲： $3 (3 x + 1) - 1 = 4 (5 x - 4)$ .
乙： $9 x + 3 - 1 = 20 x - 16$ .
丙： $9 x - 20 x = - 16 - 3 + 1$ .
丁： $- 11 x = - 20$ .
戊： $x = - \frac{20}{11}$ .

(1)、在“接力游戏”中，乙同学是根据进行变形的.（填序号）
①等式的性质 ②乘法分配律

(2)、在“接力游戏”中，自己负责的一步出现错误的是.

(3)、请写出正确的求解过程.

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 低碳环保的新能源汽车深受广大市民的喜爱，市场销售火爆.某工厂为了加快新能源汽车零件的生产速度，决定购进甲、乙两种型号的新设备进行零件加工，已知每台甲型设备比每台乙型设备每天多加工5个零件，若20台甲型设备和15台乙型设备每天共加工零件1150个，则每台甲型设备和每台乙型设备每天分别加工零件多少个？

查看试题解析
20. 某电影院地面的一部分是扇形，观众席每排的坐位数如下表：
排数 1 2 3 4 5 …
座位数 50 54 58 62 66 …
按这种方式排下去.

(1)、第7排、第8排各有多少个座位？

(2)、第n，（ $n \geq 1$ ，且为正整数）排有多少个座位？

(3)、若某排有110个座位，则该排的排数是多少？

查看试题解析

六、（本题满分12分）

21. 有一列单项式，按一定规律排列成： $- x$ ， $2 x^{2}$ ， $- 4 x^{3}$ ， $8 x^{4}$ ， $- 16 x^{5}$ ， ….根据其中的规律，回答问题.

(1)、第8个单项式是，第n，（ $n \geq 2$ ，且为正整数）个单项式是.

(2)、若某三个相邻的单项式的系数之和是 $- 768$ ，则这三个单项式分别是多少？

查看试题解析

七、（本题满分12分）

22. 定义：如果两个一元一次方程的解之和为1，那么就称这两个方程互为“美美与共方程”.例如：方程 $2 x - 1 = 3$ 的解为 $x = 2$ ，方程 $x + 1 = 0$ 的解为 $x = - 1$ ，两个方程的解之和为1，所以这两个方程互为“美美与共方程”.

(1)、请判断方程 $4 x - (x + 5) = 1$ 与方程 $- 2 x - x = 9$ 是否互为“美美与共方程”.

(2)、若关于的方程 $2 x + 3 m = 1$ 与方程 $\frac{5 x - 1}{2} = \frac{3 x + 1}{6} + \frac{5 x - 1}{3}$ 互为“美美与共方程”，求 $m$ 的值.

查看试题解析

八、（本题满分14分）

23. 为满足不同学生个性化课后服务需求，助力“双减”政策落地生根，某初中开展了丰富多彩的小组活动.下表是几位同学某学期参加的课外兴趣小组的活动时间统计表，其中同一兴趣小组每次活动时间相同.

参与小组活动总时间/h
科技小组活动次数
体育小组活动次数
小华
23
7
6
小青
21
6
6
小丽
10.5

小睿

(1)、求科技小组每次活动的时间和体育小组每次活动的时间.

(2)、求小丽参加小组活动的总次数.

(3)、在一次聊天中，小睿说她参加科技小组和体育小组活动共14次，且参加科技小组的活动时长刚好是参加体育小组活动时长的一半.请你通过计算，判断小容的话是否属实.

查看试题解析

	参与小组活动总时间/h	科技小组活动次数	体育小组活动次数
小华	23	7	6
小青	21	6	6
小丽	10.5
小睿

排数	1	2	3	4	5	…
座位数	50	54	58	62	66	…