黑龙江省哈尔滨市巴彦县2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-01-16 类型：期末考试

进入出卷网下载

一、选择题（每题3分，计30分．每题只有一个正确的答案）

1. $- \sqrt{5}$ 的相反数是（）

A、 $- \sqrt{5}$ B、 $\sqrt{5}$ C、 $- \frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
2. 下列计算中正确的是（）

A、 $2 a^{3} - a^{2} = a$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 $a^{3} \div a^{2} = 1$ D、 ${(a^{3})}^{2} = a^{5}$

查看试题解析
3. 下列与杭州亚运会有关的图案中，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
4. 如图是一个由5个相同的小正方体组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 若反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，-5），则该反比例函数的图象位于（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 1 ， B C = 2$ ，那么 $c o s A$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2}{5} \sqrt{5}$

查看试题解析
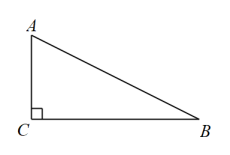7. “绿色电力，与你同行”，根据中国汽车工业协会发布的数据显示，我国新能源汽车销售量逐年增加，据统计2022年新能源汽车年销售量为 $700$ 万辆，预计2024年新能源汽车年销售量将达到 $1372$ 万辆．则这两年新能源汽车销售量年平均增长率为（）

A、 $55 %$ B、 $50 %$ C、 $45 %$ D、 $40 %$

查看试题解析
8. 将抛物线 $y = 2 {(x - 1)}^{2} + 3$ 的图象向左平移1个单位，再向下平移3个单位，平移后所得抛物线的解析式为（）

A、 $y = 2 x^{2}$ B、 $y = 2 x^{2} + 6$ C、 $y = 2 {(x - 2)}^{2}$ D、 $y = 2 {(x - 2)}^{2} + 6$

查看试题解析
9. 如图，是某商店售卖的花架简图，其中 $A D ∥ B E ∥ C F$ ， $D E = 24 c m$ ， $E F = 40 c m$ ， $B C = 50 c m$ ，则 $A B$ 长为（） $c m$ ．

A、 $\frac{80}{3}$ B、 $\frac{100}{3}$ C、50 D、30

查看试题解析
10. 如图是一种轨道示意图，其中 $A D C$ 和 $A B C$ 均为半圆，点M，A，C，N依次在同一直线上，且 $A M = C N$ ．现有两个机器人（看成点）分别从M，N两点同时出发，沿着轨道以大小相同的速度匀速移动，其路线分别为 $M \to A \to D \to C \to N$ 和 $N \to C \to B \to A \to M$ ．若移动时间为x，两个机器人之间距离为y，则y与x关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每小题3分，共计30分）

11. “多少事，从来急；天地转，光阴迫．一万年太久，只争朝夕．”伟人通过这首《满江红·和郭沫若同志》告诉我们青年学生：要珍惜每分每秒；努力工作，努力学习．一天时间为86400秒，用科学记数法表示这一数字是．

查看试题解析
12. 函数 $y = \frac{x + 9}{2 x + 6}$ 中，自变量x的取值范围是．

查看试题解析
13. 一元二次方程 $x^{2} ﹣ x ﹣ 1 ＝ 0$ 的根是.

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ A C B = 90^{\circ}$ ， $C D ⊥ A B$ ，垂足为D，若AD=2，BD=4，则CD为．

查看试题解析
15. 如图，在 $⊙ O$ 中，直径 $A B$ ，弦 $C D$ 相交于点 $P$ ．连接 $O C$ ．且 $O C ⊥ A B$ ，若 $∠ A = 20 °$ ，则 $∠ B P D$ 的度数为．

查看试题解析
16. 如图，在 $▱ A B C D$ 中， $∠ D = 60 °$ ．以点 $B$ 为圆心，以 $B A$ 的长为半径作弧交边 $B C$ 于点 $E$ ，连接 $A E$ ．分别以点 $A ， E$ 为圆心，以大于 $\frac{1}{2} A E$ 的长为半径作弧，两弧交于点 $P$ ，作射线 $B P$ 交 $A E$ 于点 $O$ ，交边 $A D$ 于点 $F$ ，则 $\frac{O F}{O E}$ 的值为．

查看试题解析
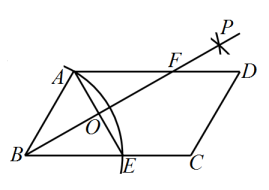17. 已知扇形的圆心角度数为 $120 °$ ，面积为 $12 π$ ，则该扇形的弧长为．

查看试题解析
18. 某校冬季选修课深受学生喜欢，小冰和小城从“滑冰、冰壶、雪地足球、冰尜”中任选一门学习，两人恰好都选到“冰尜”的概率的是．

查看试题解析
19. 已知在平行四边形 $A B C D$ 中，点E，F分别是 $A B ， C D$ 的中点，点P为直线 $B C$ 上一点， $P A$ 交 $E F$ 于点G，若 $B C = 13 ， C P = 1$ ．则线段 $E G$ 的长为．

查看试题解析
20. 如图，在矩形 $A B C D$ 中， $A B = 10$ ，点O是对角线的交点，点E，F分别是 $A B ， B C$ 上的点， $A E = 6$ ，点G为 $E F$ 的中点，连接 $O E ， O G$ ， $O G = 5 ， ∠ A E O - ∠ E O G = 2 ∠ E F B$ ．则线段 $E F$ 的长度为．

查看试题解析

三、解答题：（共60分）

21. 先化简，再求值： $(1 - \frac{4}{x + 1}) \div \frac{x^{2} - 9}{x + 3}$ ，其中 $x = 2 s i n 60 ° - t a n 45 °$ ．

查看试题解析
22. 如图，方格纸中每个小正方形的边长均为1， $△ A B C$ 的顶点和线段 $D E$ 的端点均在小正方形的顶点上．

(1)、在图中画出以点A为旋转中心，把 $△ A B C$ 绕着点A逆时针旋转 $90 °$ ，得到的 $△ A B^{'} C^{'}$ ；（点B的对应点为 $B^{'}$ ，点C的对应点为 $C^{'}$ ）．

(2)、在图中画出以 $D E$ 为边的四边形 $D E F G$ ，四边形 $D E F G$ 为中心对称图形且一边长为 $\sqrt{10}$ ，连接 $C^{'} G$ ，请直接写出线段 $C^{'} G$ 的长．

查看试题解析
23. 某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图1所示．

(1)、如图2，在 $P$ 点观察所测物体最高点 $C$ ，当量角器零刻度线上 $A ， B$ 两点均在视线 $P C$ 上时，测得视线与铅垂线所夹的锐角为 $α$ ，设仰角为 $β$ ，请直接用含 $α$ 的代数式示 $β$ ．

(2)、如图3，为了测量广场上空气球 $A$ 离地面的高度，该小组利用自制简易测角仪在点 $B ， C$ 分别测得气球 $A$ 的仰角 $∠ A B D$ 为 $37 °$ ， $∠ A C D$ 为 $45 °$ ，地面上点 $B ， C ， D$ 在同一水平直线上， $B C = 20 m$ ，求气球 $A$ 离地面的高度 $A D$ ．（参考数据： $s i n 37 ° \approx 0.60 ， c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ）

查看试题解析
24. 如图1，已知四边形 $A B C D$ 是菱形，点E，F在对角线 $B D$ 上， $B E = D F$ ．

(1)、求证： $∠ B A E = ∠ D A F$ ；

(2)、如图2，若 $A F ⊥ B A$ ，点E为 $B F$ 的中点，连接 $A C$ 交 $B D$ 于点O，连接 $C F$ 并延长交 $A D$ 于点G，在不添加任何辅助线情况下，请直接写出图2中等于线段 $O E$ 的 $\sqrt{3}$ 倍的四条线段．

查看试题解析
25. 2023年12月18日，以“龙腾冰雪逐梦亚冬”为主题的第二十五届哈尔滨冰雪大世界开园，某商场购置A，B两种冰雪大世界纪念玩具，其中B玩具的单价比A玩具的单价贵25元，且购置2个B玩具与1个A玩具共花费200元．

(1)、求A，B玩具的单价？

(2)、若该商场要求购置B玩具的数量是A玩具数量的2倍，且购置玩具的总额不高于20000元，则该商场最多可以购置多少个A玩具？

查看试题解析
26. 如图1， $△ A B C$ 内接于 $⊙ O$ ， $B C$ 为直径，点D为 $⊙ O$ 上一点，连接 $C D$ 交 $A B$ 于点G， $A E ⊥ C D$ 于点F交 $⊙ O$ 于点E．

(1)、求证： $∠ F A G = ∠ F C A$ ；

(2)、如图2，连接 $B F 、 B E$ ，若 $B F = B E$ ，求证： $D G = F G$ ；

(3)、在（2）的条件下，如图3，点H是 $C D$ 上一点，连接 $E H$ ， $∠ F E H = \frac{1}{2} ∠ A B C ， B C - F H = 4 D G$ ，若 $S_{△ B C F} = \frac{3 \sqrt{3}}{2}$ ，求线段 $B F$ 的长．

查看试题解析
27. 如图1，在平面直角坐标系中，O为坐标原点，抛物线 $y = x^{2} + b x + c$ 与x轴负半轴交于点B，与x轴正半轴于点 $A (3 ， 0)$ ，交y轴于点C，连接 $A C$ ， $t a n ∠ O A C = 1$ ．

(1)、求抛物线的解析式：

(2)、如图2，点P为第三象限抛物线上一点，连接 $P B$ ， $P O$ ，若设 $△ P O B$ 的面积为S，点P的横坐标为t，求S与t的函数关系式（不要求写出自变量t的取值范围）；

(3)、在（2）的条件下，如图3，过点P作 $P E ⊥ x$ 轴于点E，点K为抛物线的顶点，连接 $B K$ 交 $P E$ 于点F，点D为 $A K$ 上一点， $B F = D K$ ，连接 $D F$ ，若 $∠ E B F - ∠ D F K = 45 °$ ，求点P的坐标．

查看试题解析