黑龙江省绥化市望奎县2023-2024学年九年级(五四制)上学期期末数学试题
试卷更新日期:2024-01-16 类型:期末考试
一、选择题(每小题3分,共36分)
-
1. 下列四个图中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定( )A、与x轴相切,与y轴相切 B、与x轴相切,与y轴相交 C、与x轴相交,与y轴相切 D、与x轴相交,与y轴相交3. 下列事件属于随机事件的是( )A、常压下,温度降到以下,自来水会结冰 B、随意打开一本书,书的页码是奇数 C、任意一个五边形的外角和等于 D、如果 , 那么4. 若关于的方程的一个根是 , 则另一个根及的值分别是( )A、 B、 C、 D、5. 如图,点O是内切圆的圆心,已知 , 则的度数是( )
2. 在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定( )A、与x轴相切,与y轴相切 B、与x轴相切,与y轴相交 C、与x轴相交,与y轴相切 D、与x轴相交,与y轴相交3. 下列事件属于随机事件的是( )A、常压下,温度降到以下,自来水会结冰 B、随意打开一本书,书的页码是奇数 C、任意一个五边形的外角和等于 D、如果 , 那么4. 若关于的方程的一个根是 , 则另一个根及的值分别是( )A、 B、 C、 D、5. 如图,点O是内切圆的圆心,已知 , 则的度数是( )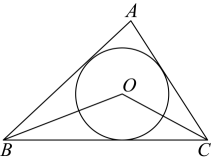 A、 B、 C、 D、6. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 如图,函数和是常数,且在同一个平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、6. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 如图,函数和是常数,且在同一个平面直角坐标系中的图象可能是( )A、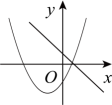 B、
B、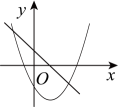 C、
C、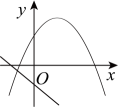 D、
D、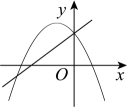 8. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )
8. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )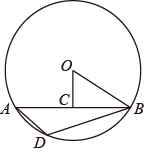 A、 B、 C、 D、9. 某宾馆有50个房间供游客居住,当每间房每天的价格为120元时,房间会全部住满,当价格每增加10元时,就会有一个房间空闲,已知宾馆每天需对当天居住的每个房间支出30元的相关费用,设当天房价定为元/间,若宾馆每天利润为5000元,则可列方程为( )A、 B、 C、 D、10. 如图,AB是的直径,弦CD交AB于点P, , , , 则CD的长为( )
A、 B、 C、 D、9. 某宾馆有50个房间供游客居住,当每间房每天的价格为120元时,房间会全部住满,当价格每增加10元时,就会有一个房间空闲,已知宾馆每天需对当天居住的每个房间支出30元的相关费用,设当天房价定为元/间,若宾馆每天利润为5000元,则可列方程为( )A、 B、 C、 D、10. 如图,AB是的直径,弦CD交AB于点P, , , , 则CD的长为( )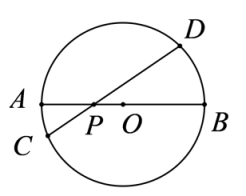 A、 B、 C、 D、811. 如图,在等腰中, , , 边在轴上,将绕原点逆时针旋转 , 得到 , 若 , 则点的对应点的坐标为( )
A、 B、 C、 D、811. 如图,在等腰中, , , 边在轴上,将绕原点逆时针旋转 , 得到 , 若 , 则点的对应点的坐标为( )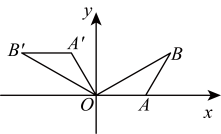 A、 B、 C、 D、12. 如图;二次函数的图象与轴分别交于 , 两点,与轴正半轴交于点C,下列判断:;;;;若 , 是拋物线上的两个点,则 , 其中正确的是( )
A、 B、 C、 D、12. 如图;二次函数的图象与轴分别交于 , 两点,与轴正半轴交于点C,下列判断:;;;;若 , 是拋物线上的两个点,则 , 其中正确的是( )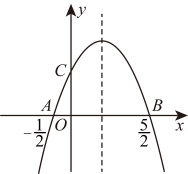 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共30分)
-
13. 在平面直角坐标系中,点关于原点对称的点的坐标为 .14. 将二次函数转化为的形式为 .15. 把标号为的三个小球放入一个不透明的袋子中,随机摸取一个小球然后放回,再随机摸出一个小球,两次摸出的小球标号的和大于的概率是 .16. 若关于的二次函数的图象与轴有2个公共点,则的取值范围是 .17. 在实数范围内定义一种运算“*”,其规则为 a*b=a(a﹣b),根据这个规则,方程(x+2)*5=0 的解为 .18. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
19. 圆锥的母线长为 , 高为 , 则该圆锥侧面展开图的圆心角为 .20. 如图,圆内接正方形的边长与外切正方形的边长之比是 .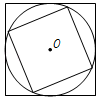 21. 如图,将绕点逆时针旋转 , 得到 , 连接 , 若 , 则的度数为 .
21. 如图,将绕点逆时针旋转 , 得到 , 连接 , 若 , 则的度数为 .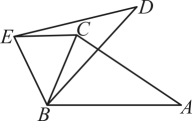 22. 在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
22. 在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .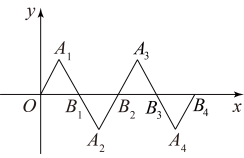
三、解答题(共54分)
-
23. 解方程:(1)、(用配方法);(2)、 .24. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围.(2)、若该方程的两个实数根为 、 ,且 ,求 的值.25. 如图,正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2),B(5,5),C(1,1)均在格点上.
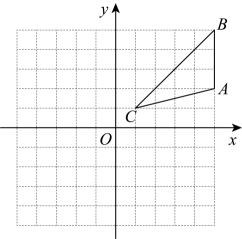 (1)、将△ABC向下平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;(2)、画出△A1B1C1绕点C1逆时针旋转90°后得到的△A2B2C1;(3)、在(2)的条件下,求△A1B1C1扫过的面积.26. 为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有:A . 回顾重要事件;B . 列举革命先烈;C . 讲述英雄故事;D . 歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)、将△ABC向下平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;(2)、画出△A1B1C1绕点C1逆时针旋转90°后得到的△A2B2C1;(3)、在(2)的条件下,求△A1B1C1扫过的面积.26. 为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有:A . 回顾重要事件;B . 列举革命先烈;C . 讲述英雄故事;D . 歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题: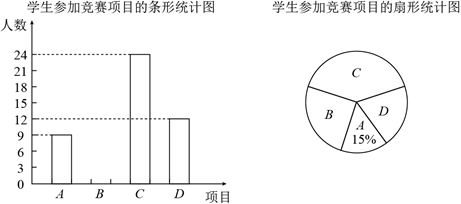 (1)、本次被调查的学生共有名;(2)、在扇形统计图中“B项目”所对应的扇形圆心角的度数为 ▲ ,并把条形统计图补充完整;(3)、从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.
(1)、本次被调查的学生共有名;(2)、在扇形统计图中“B项目”所对应的扇形圆心角的度数为 ▲ ,并把条形统计图补充完整;(3)、从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.