黑龙江省齐齐哈尔市梅里斯达斡尔族区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-01-16 类型：期末考试

进入出卷网下载

一、选择题（每小题只有一个正确答案，每小题3分，共30分）

1. 下列运算中，正确的是（）

A、 $x^{3} \cdot x^{2} = x^{5}$ B、 $x + x^{2} = x^{3}$ C、 $2 x^{3} \div x^{2} = x$ D、 ${(\frac{x}{2})}^{3} = \frac{x^{3}}{2}$

查看试题解析
2. 在以下节水、绿色食品、质量安全、可回收物等四个标志中，是轴对称图形的有（）个．

A、1 B、2 C、3 D、4

查看试题解析
3. 等腰三角形的周长为13cm，其中一边长为3cm．则该等腰三角形的底长为（）

A、3 cm或5 cm B、3 cm或7 cm C、3 cm D、5 cm

查看试题解析
4. 把分式 $\frac{x}{x - y}$ 中的x，y的值都扩大3倍，那么分式的值是（　　）

A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的 $\frac{1}{3}$

查看试题解析
5. 若二次三项式 $4 x^{2} + m x y + 9 y^{2}$ 是一个完全平方式，则 $m$ 的可能值是（）

A、±6 B、12 C、6 D、±12

查看试题解析
6. 如图，△ABC是一张三角形纸片，∠C＝90°，∠A＝36°，将△ABC折叠，使点B与点A重合，折痕为DE，连接BD，则∠CBD的度数为（　　）

A、16° B、18° C、15° D、17°

查看试题解析
7. 若一个正多边形的一个内角与它相邻的外角的比是 $5 ： 1$ ，则这个正多边形的边数为（）

A、14 B、12 C、10 D、8

查看试题解析
8. “绿水青山就是金山银山”.为改造太湖水质，某工程队对2400平方公里的水域进行水质净化，实际工作时每天的工作效率比原计划提高了20%，结果提前了40天完成任务.设实际每天净化的水域面积为x平方公里，则下列方程中正确的是（）

A、 $\frac{2400}{x} - \frac{2400}{(1 + 20 %) x} = 40$ B、 $\frac{2400}{x} - \frac{2400 \times (1 + 20 %)}{x} = 40$ C、 $\frac{2400 \times (1 + 20 %)}{x} - \frac{2400}{x} = 40$ D、 $\frac{2400}{(1 + 20 %) x} - \frac{2400}{x} = 40$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C ， △ A B C$ 的面积为 $16 ， B C = 4$ ，分别以点 $A 、 B$ 为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧分别交于 $E ， F$ ，连接 $E F ， D$ 为 $B C$ 的中点， $M$ 为直线 $E F$ 上任意一点．则 $B M + M D$ 长度的最小值为（）

A、 $6$ B、 $8$ C、 $10$ D、 $12$

查看试题解析
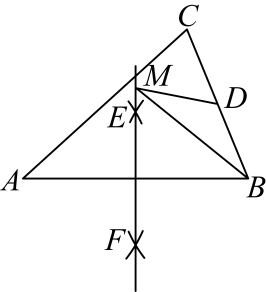10. 如图，已知 $△ A B C$ 是等边三角形，点D、E分别在边AB、BC上，CD、AE交于点F， $∠ A F D = 60 °$ ． FG为 $△ A F C$ 的角平分线，点H在FG的延长线上， $H G = C D$ ，连接HA、HC．① $B D = C E$ ；② $∠ A H C = 60 °$ ；③ $F C = C G$ ；④ $S_{△ C B D} = S_{△ C G H}$ ；其中说法正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共21分）

11. 一个氧原子的直径为0.000000000148m，用科学记数法表示为m.

查看试题解析
12. 若分式 $\frac{2 x + 1}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
13. 分解因式3x²﹣27y²＝.

查看试题解析
14. 将一副三角尺按如图的方式拼摆，则 $∠ C E D$ 的度数为 $°$ ．

查看试题解析
15. 在△ABC中， AB=AC，∠BAC=100°，点D在BC边上，连接AD，若△ABD为直角三角形，则∠ADC的度数为.

查看试题解析
16. 若关于x的分式方程 $\frac{1}{x + 3} - 1 = \frac{a}{x + 3}$ ，有负数解，则实数a的取值范围是．

查看试题解析
17. 如图，已知∠AOB=90°，点A绕点O顺时针旋转后的对应点A₁落在射线OB上，点A绕点A₁顺时针旋转后的对应点A₂落在射线OB上，点A绕点A₂顺时针旋转后的对应点A₃落在射线OB上，…，连接AA₁ ， AA₂ ， AA₃…，依此作法，则∠AA_nA_n₊₁等于度．（用含n的代数式表示，n为正整数）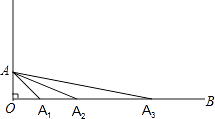

查看试题解析

三、解答题（共49分）

18. 计算：

(1)、 ${(\frac{1}{2})}^{3} + {(- 5)}^{0} - {(- \frac{1}{4})}^{- 2}$

(2)、 $[x (x^{2} y^{2} - x y) - y (x^{2} - x^{3} y)] \div 2 x^{2} y$

查看试题解析
19.

(1)、先化简，再求值： $\frac{x^{2} - 6 x + 9}{x^{2} - 1} \div \frac{x^{2} - 3 x}{x + 1}$ ，其中， $x = - 3$ ．

(2)、解方程： $\frac{x}{x + 1} = \frac{2 x}{3 x + 3} - 1$

查看试题解析
20. 如图所示，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

(1)、在图中画出△ABC关于y轴的对称图形△A₁B₁C₁ ，写出A₁、B₁、C₁的坐标；

(2)、画出两条线段，将△ABC分成面积相等的三部分，要求所画线段的端点在格点上．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D， $C E ⊥ A D$ ，分别交 $A B 、 A D$ 于点E、F．

(1)、求证： $E F = C F$ ；

(2)、若 $∠ A C B = 80 °$ ， $∠ B C E = 30 °$ ，求 $∠ A B C$ 的度数．

查看试题解析
22. 在△ABC中，∠ACB＝90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

(1)、当直线MN绕点C旋转到图1的位置时，求证：①ADC≌△CEB．②DE=AD+BE；

(2)、当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．

查看试题解析
23. 荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．

(1)、求购买该品牌一个台灯、一个手电筒各需要多少元？

(2)、经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， $B C = 18 c m$ ．动点 $P$ 从点 $A$ 出发，沿 $A B$ 向点 $B$ 运动，动点 $Q$ 从点 $B$ 出发，沿 $B C$ 向点 $C$ 运动，如果动点 $P$ 以 $2 c m / s$ ， $Q$ 以 $1 c m / s$ 的速度同时出发，一个动点停止后，另一个动点随之停止运动，设运动时间为 $t (s)$ ，解答下列问题：

(1)、求 $t$ 为何值时， $△ P B Q$ 是等边三角形；

(2)、 $P$ ， $Q$ 在运动过程中， $△ P B Q$ 的形状不断发生变化，当 $t$ 为何值时， $△ P B Q$ 是直角三角形？并说明理由．

查看试题解析