广东省深圳市2023-2024学年第一学期八年级数学期末模拟练习卷

试卷更新日期：2024-01-16 类型：期末考试

进入出卷网下载

一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1. 9的算术平方根是（）

A、±3 B、﹣3 C、3 D、±81

查看试题解析
2. 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（）

A、﹣5 B、﹣3 C、3 D、1

查看试题解析
3. 某企业车间有 $20$ 名工人，某一天他们生产的机器零件个数统计如表：
零件个数（个）
6
7
8
人数（人）
9
8
3
表中表示零件个数的数据中，众数、中位数分别是（　　）

A、7个，7个 B、6个，7个 C、 $12$ 个， $12$ 个 D、8个，6个

查看试题解析
4. 如图，将长方形纸片ABCD沿对角线BD折叠，点C的对应点为E，
若∠CBD＝35°，则∠AFB的度数为（　　）

A、70° B、75° C、80° D、85°

查看试题解析
5. 若函数 $y = k x + k$ （k为常数，且 $k \neq 0$ ）中，y随x的增大而增大，则其图像可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图，为了测算出学校旗杆的高度，小明将升旗的绳子拉到旗杆底端，并在与旗杆等长的地方打了一个结，然后将绳子底端拉到离旗杆底端5米的地面某处，发现此时绳子底端距离打结处约1米，则旗杆的高度是（）

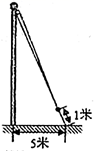A、12 B、13 C、15 D、24

查看试题解析
7. 如图，△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线交AC于D，交AB于E，CD＝3，则AD等于（　　）

A、12 B、10 C、8 D、6

查看试题解析
8. 《九章算术》中记载一题目，译文如下，今有人合伙购物，每人出8钱，会多3钱；
每人出7钱，又会差4钱，问人数、物价各是多少？设合伙人数为 $x$ 人，物价为 $y$ 钱，
以下列出的方程组正确的是（　　）

A、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ 7 x - y = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ y - 7 x = 4 \end{array}$ D、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A D$ 平分 $∠ B A C$ ， $D E$ 垂直平分 $A C$ ，若 $A B = \sqrt{3}$ ，则 $D E$ 的值为（　　）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、1 D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
10. 甲、乙两车从A地出发，沿同一路线驶向B地. 甲车先出发匀速驶向B地，40 min后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时. 由于满载货物，为了行驶安全，速度减少了50 km/h，结果与甲车同时到达B地. 甲乙两车距A地的路程y（km）与乙车行驶时间x（h）之间的函数图象如图所示，则下列说法：①a＝4.5；②甲的速度是60 km/h；③乙出发80 min追上甲；④乙刚到达货站时，甲距B地180 km.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本部分共5小题，每小题3分，共15分，请将正确的答案填在答题卡上）．

11. 计算： $\frac{\sqrt{32} - \sqrt{8}}{\sqrt{2}}$ = ．

查看试题解析
12. 若点 $A (- 3 ， y_{1})$ ， $B (2 ， y_{2})$ 都在一次函数 $y = - x + 1$ 的图象上，则 $y_{1}$ $y_{2}$ ．（填“ $>$ ”或“ $<$ ”）

查看试题解析
13. 一次函数 $y = k x + b$ 与 $y = x - 2$ 的图象如图所示，则关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} y = k x + b \\ y = x - 2 \end{array}$ 的解是．

查看试题解析
14. 有一个数值转换器，流程如下：
当输入的x值为 $64$ 时，输出的y值是．

查看试题解析
15. 如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，若CD＝1，则BD的长是．

查看试题解析

三、解答题（本大题共7题．共55分.解答应写出文字说明、演算步骤或证明过程）．

16. 计算：

(1)、 $| \sqrt{2} - 2 | - \sqrt[3]{8} + {(\frac{1}{3})}^{- 1}$

(2)、 ${(1 - \sqrt{3})}^{2} + (\sqrt{3} + 2) (\sqrt{3} - 2)$

查看试题解析
17. 解方程组

(1)、 ${\begin{array}{l} x - y = 10 \\ 2 x + y = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x + 2 y = 15 \\ 5 x + 4 y = 35 \end{array}$ ．

查看试题解析
18. 如图，网格中小正方形的边长为1，

(1)、画出△ABC关于x轴对称的△A₁B₁C₁（其中A₁、B₁、C₁分别为A、B、C的对应点）；

(2)、△ABC的面积为；点B到边AC的距离为；

(3)、在x轴上是否存在一点M，使得MA＋MB最小，若存在，请直接写出MA＋MB的最小值；若不存在，请说明原因

查看试题解析
19. 某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，
学生课外阅读的数量最少的是 $5$ 本，最多的是 $8$ 本，并根据调查结果绘制了如图不完整的图表．

(1)、补全条形统计图，扇形统计图中的 $a =$ ▲ ．

(2)、本次抽样调查中，中位数是，扇形统计图中课外阅读 $6$ 本的扇形的圆心角大小为度；

(3)、若该校八年级共有 $1200$ 名学生，请估计该校八年级学生课外阅读至少 $7$ 本的人数．

查看试题解析
20. 五和超市购进 $A$ 、 $B$ 两种饮料共200箱，两种饮料的成本与销售价如下表：

饮料

成本（元/箱）

销售价（元/箱）

$A$

25

35

$B$

35

50

(1)、若该超市花了6500元进货，求购进 $A$ 、 $B$ 两种饮料各多少箱？

(2)、设购进 $A$ 种饮料 $a$ 箱（ $50 \leq a \leq 100$ ），200箱饮料全部卖完可获利润 $W$ 元，求 $W$ 与 $a$ 的函数关系式，并求购进 $A$ 种饮料多少箱时，可获得最大利润，最大利润是多少？

查看试题解析
21. nbsp；.甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．

(1)、 $A ， B$ 两城相距千米；

(2)、求出乙车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系式；

(3)、求甲乙两车相遇时甲车行驶的时间以及此时距离A城的距离．

查看试题解析
22. 如图，直线l₁：y＝x＋3与过点A（3，0）的直线l₂交于点C（1，m），与x轴交于点B．

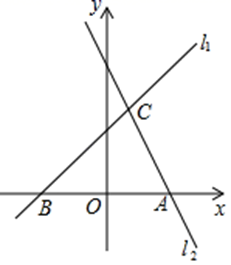(1)、求直线l₂的解析式；

(2)、点M在直线l₁上，MN∥y轴，交直线l₂于点N，若MN＝AB，求点M的坐标．

(3)、在x轴上是否存在点P，使以B、C、P为顶点的三角形是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

饮料	成本（元/箱）	销售价（元/箱）
$A$	25	35
$B$	35	50

零件个数（个）	6	7	8
人数（人）	9	8	3