广东省广州市2023-2024学年第一学期七年级数学期末考前练习卷

试卷更新日期：2024-01-16 类型：期末考试

进入出卷网下载

一、单选题（本大题共10小题，每小题3分，共30分）

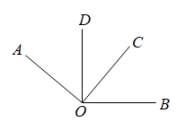
1. $- 2023$ 的相反数是（）

A、2023 B、 $\frac{1}{2013}$ C、 $- \frac{1}{2013}$ D、 $- 2023$

查看试题解析
2. 2022年2月4日，北京第二十四届冬季奥林匹克运动会开幕式在国家体育场隆重举行，中国大陆地区观看人数约316000000人．用科学记数法表示316000000是（）

A、3.16×10⁷ B、31.6×10⁷ C、3.16×10⁸ D、0.316×10⁹

查看试题解析
3. 关于x的方程 $2 (x - a) = 6$ 的解是 $x = 1$ ，则a的值为（）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
4. 若 $- a^{n + 4} b^{6}$ 与 $3 a^{2} b^{2 m}$ 是同类项，则 $n^{m}$ 的值是（）

A、 $- 8$ B、 $- 6$ C、8 D、9

查看试题解析
5. 下列方程变形正确的是（）

A、由 $- 2 x = 1$ 得 $x = - 2$ B、由 $x - 1 = 3$ 得 $x = 3 - 1$ C、由 $- \frac{3}{2} x = 1$ 得 $x = - \frac{2}{3}$ D、由 $x + 2 = 7$ 得 $x = 7 + 2$

查看试题解析
6. 如图，将一副三角板叠在一起，使它们的直角顶点重合于O点，已知∠AOB =160°，则∠COD的度数为（）

A、20° B、30° C、40° D、50°

查看试题解析
7. 如图是某月份的日历表，任意框出同一列上的三个数，则这三个数的和不可能是（）

A、39 B、43 C、57 D、66

查看试题解析
8. 有理数 $a$ ， $b$ 在数轴上对应的点的位置如图所示，对于下列四个结论：
$① b - a > 0$ ； $② | a | < | b |$ ； $③ a + b > 0$ ； $④ \frac{a}{b} > 0 .$ 其中正确的是（）

A、 $① ② ③ ④$ B、 $① ② ③$ C、 $① ③ ④$ D、 $② ③ ④$

查看试题解析
9. 某个体商贩在一次买卖中，同时卖出两件上衣，售价都是135元，若按成本计，其中一件盈利25%，另一件亏本25%，在这次买卖中他（）．

A、不赚不赔 B、赚9元 C、赔18元 D、赚18元

查看试题解析
10. 用火柴棒按如图的方式搭一行三角形，搭一个三角形需3支火柴棒，搭2个三角形需5支火柴棒，搭3个三角形需7支火柴棒，照这样的规律，搭2022个三角形需要火柴棒（）

A、4040支 B、4045支 C、4050支 D、4055支

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. $- \frac{2}{3}$ 的倒数是.

查看试题解析
12. 若|a-2|+（b+3）²=0，则 $b^{a}$ = ．

查看试题解析
13. 已知长方形的周长为 $4 a + 2 b$ ，其一边长为 $a + b$ ，则另一边长为．

查看试题解析
14. 已知，如图 $∠ C O D = 40 ° ， ∠ A O C = ∠ B O D = 90 °$ ，则 $∠ A O B =$ 度．

查看试题解析
15. 幻方历史悠久，最早出现在夏禹时代的“洛书”就是三阶幻方，其中每行、每列、每条对角线上的三个数之和都是相等的，如图所示的三阶幻方中a的值是

查看试题解析
16. 为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示，按照这样的规律，摆第n个图，需用火柴棒的根数为.

查看试题解析

三、解答题（本大题共72分）解答应写出文字说明、推理过程或演算步骤．

17. 计算：

(1)、 $24 \times (- \frac{5}{6} + \frac{3}{8} - \frac{1}{12})$ ；

(2)、 $- 1^{4} + {(- 2)}^{3} ÷ 4 × [5 - {(- 3)}^{2}]$ ．

查看试题解析
18. 解方程： $\frac{2 x + 1}{3} - \frac{x - 1}{3} = 4$ ．

查看试题解析
19. 先化简，再求值； $2 (a^{2} - 2 a) - (a - 2)$ ，其中 $a = - 1$ ．

查看试题解析
20. 已知：如图，点O在直线AC上，OD平分∠AOB， $∠ B O E = \frac{1}{2} ∠ E O C ， ∠ D O E = 70^{\circ}$ ，求：∠EOC的度数．

查看试题解析
21. 如图，已知A、B、C、D四个点．

(1)、①画直线AB、CD相交于点P；
②连接AC和BD并延长AC和BD相交于点Q；
③连接AD、BC相交于点O；

(2)、以点C为端点的射线有条；

(3)、以点C为一个端点的线段有条．

查看试题解析
22. 国庆节期间，甲、乙两商场以相同价格出售同样的商品，并且各自推出不同的优惠方案：在甲商场累计购物超过300元后，超出的部分打八五折收费；在乙商场累计购物超过200元后，超出的部分打九折收费．设小华预计累计购物x元（ $x > 300$ ）．

(1)、计算一下，小华预计累计购物多少元商品时，到两个商场购物实际所付的费用相同？

(2)、如果小华预计累计购物600元的商品，她选哪个商场购物比较合适？说明理由．

查看试题解析
23. 如图，四边形 $A B C D$ 是一个长方形．

(1)、根据图中数据，用含 $x$ 的代数式表示阴影部分的面积 $S$ ；

(2)、当 $x = 4$ 时，求 $S$ 的值．

查看试题解析
24. 如图，已知数轴上 $A$ 、 $B$ 两点所表示的数分别为 $- 3$ 和 $9$ ．

(1)、求线段 $A B$ 的长；

(2)、当点 $P$ 为线段 $A B$ 的一个动点，且 $M$ 为 $P A$ 的中点， $N$ 为 $P B$ 的中点．请你画出相应的图形，并求出线段 $M N$ 的长．

(3)、当点 $P$ 为数轴上点 $A$ 左侧的一个动点，且 $M$ 为 $P A$ 的中点， $N$ 为 $P B$ 的中点．
请你画出图形，并探究 $M N$ 的长度是否发生改变？
若不变，求出线段 $M N$ 的长；若改变，请说明理由．

查看试题解析
25. 如图， $O M$ 是 $∠ A O C$ 的平分线， $O N$ 是 $∠ B O C$ 的平分线．

(1)、如图1，当 $∠ A O B$ 是直角， $∠ B O C = 60 °$ 时，求 $∠ M O N$ 的度数是多少？

(2)、如图2，当 $∠ A O B = α$ ， $∠ B O C = 60 °$ 时，尝试发现 $∠ M O N$ 与 $α$ 的数量关系．

(3)、如图3，当 $∠ A O B = α$ ， $∠ B O C = β$ 时，猜想： $∠ M O N$ 与 $α$ 、 $β$ 有数量关系吗？直接写出结论即可．

查看试题解析