广东省汕头市潮南区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-01-16 类型:期末考试
一、选择题
-
1. 以下是我国部分博物馆标志的图案,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件为必然事件的是( )A、中秋节晚上一定能看到月亮 B、某彩票中奖率是1%,买100张彩票一定会中奖 C、明天的气温一定会比今天的高 D、地球上,上抛的篮球一定会下落3. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 一元二次方程的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,是的直径,四边形内接于 , 若 , 则的直径为( )
2. 下列事件为必然事件的是( )A、中秋节晚上一定能看到月亮 B、某彩票中奖率是1%,买100张彩票一定会中奖 C、明天的气温一定会比今天的高 D、地球上,上抛的篮球一定会下落3. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 一元二次方程的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,是的直径,四边形内接于 , 若 , 则的直径为( )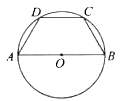 A、 B、 C、 D、6. 若关于的一元二次方程的一个根是 , 则代数式的值为( )A、 B、2023 C、 D、20247. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )
A、 B、 C、 D、6. 若关于的一元二次方程的一个根是 , 则代数式的值为( )A、 B、2023 C、 D、20247. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )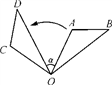 A、50° B、60° C、40° D、30°8. 已知二次函数的图象上有三点 , , , 则 , , 的大小关系为( )A、 B、 C、 D、9. 如图,四边形内接于 , 如果的度数为 , 则的度数为( )
A、50° B、60° C、40° D、30°8. 已知二次函数的图象上有三点 , , , 则 , , 的大小关系为( )A、 B、 C、 D、9. 如图,四边形内接于 , 如果的度数为 , 则的度数为( ) A、 B、 C、 D、10. 已知三角形的两条边分别是3和8,第三边是方程的根,则这个三角形的周长为( )A、17 B、18 C、17或18 D、不能确定
A、 B、 C、 D、10. 已知三角形的两条边分别是3和8,第三边是方程的根,则这个三角形的周长为( )A、17 B、18 C、17或18 D、不能确定二、填空题
-
11. 在平面直角坐标系中,点关于原点对称的点的坐标是.12. 如图,在中,弧弧 , , 点在上,连接 , , 则.
 13. 已知一个布袋里装有2个黑球、个白球,这些球除颜色外其余均相同.若从该布袋里任意摸出1个球是黑球的概率为 , 则的值为.14. 如图,是外一点,、分别和相切于点 , , 是弧上任意一点,过作的切线分别交、于点、 , 若 , 则的周长为.
13. 已知一个布袋里装有2个黑球、个白球,这些球除颜色外其余均相同.若从该布袋里任意摸出1个球是黑球的概率为 , 则的值为.14. 如图,是外一点,、分别和相切于点 , , 是弧上任意一点,过作的切线分别交、于点、 , 若 , 则的周长为. 15. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米.水面下降1米时,水面的宽度为米.
15. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米.水面下降1米时,水面的宽度为米.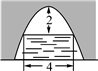 16. 如图,在平行四边形中,已知 , , , 点是边上一动点(点不与 , 重合),连接 , 作点关于直线的对称点 , 则线段的最小值为.
16. 如图,在平行四边形中,已知 , , , 点是边上一动点(点不与 , 重合),连接 , 作点关于直线的对称点 , 则线段的最小值为.
三、解答题
-
17. 用适当的方法解下列方程:.18. “阳光玫瑰”是一种优质的葡萄品种.某葡萄种植基地2020年年底已经种植“阳光玫瑰”300亩,到2022年年底“阳光玫瑰”的种植面积达到432亩.求该基地“阳光玫瑰”种植面积的年平均增长率.19. 如图,是的内切圆,与 , , 分别相切于点 , , , 若 , 求的度数.

四、解答题
-
20. 2023年第19届亚运会在杭州举办.小蔡作为亚运会的志愿者“小青荷”为大家提供咨询服务.现有如图所示“杭州亚运会吉祥物”的三盒盲盒供小蔡选择,分别记为 , , .
 (1)、小蔡从中随机抽取一盒,恰好抽到(宸宸)的概率是;(2)、小蔡从中随机抽取两盒.请用列表或画树状图的方法,求小蔡抽到的两盒吉祥物恰好是(琮琮)和(莲莲)的概率.21. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , .
(1)、小蔡从中随机抽取一盒,恰好抽到(宸宸)的概率是;(2)、小蔡从中随机抽取两盒.请用列表或画树状图的方法,求小蔡抽到的两盒吉祥物恰好是(琮琮)和(莲莲)的概率.21. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , . (1)、将绕点逆时针旋转后对应得到 , 请写出点 , , 的坐标.(2)、请在图中画出绕点顺时针旋转后的 , 并求出旋转过程中点所经过的路径长(结果保留根号和).22. 如图,矩形中,经过点 , 且与边相切于点,过边上的点 , 且.
(1)、将绕点逆时针旋转后对应得到 , 请写出点 , , 的坐标.(2)、请在图中画出绕点顺时针旋转后的 , 并求出旋转过程中点所经过的路径长(结果保留根号和).22. 如图,矩形中,经过点 , 且与边相切于点,过边上的点 , 且. (1)、求证:与相切;(2)、若 , , 求的长.
(1)、求证:与相切;(2)、若 , , 求的长.五、解答题
-
23. 鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点 , 守门员位于点 , 的延长线与球门线交于点 , 且点 , 均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离与离地高度的鹰眼数据如表:


0
9
12
15
18
21
…
图1
图2
0
4.2
4.8
5
4.8
4.2
…
(1)、根据表中数据可得,当时,达到最大值;(2)、求关于的函数解析式;(3)、当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度时,视为防守成功,若一次防守中,守门员位于足球正下方时, , 请问这次守门员能否防守成功?试通过计算说明.24. 圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形. (1)、如图1,四边形为等邻边圆内接四边形, , , 直接写出的度数;(2)、如图2,四边形内接于 , 为的直径, , , 若四边形为等邻边圆内接四边形, , 求的长.(3)、如图3,四边形为等邻边圆内接四边形, , 为的直径,且.设 , 四边形的周长为 , 试确定与的函数关系式,并求出的最大值.25. 在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于点 , 过点 , 且顶点的坐标为.
(1)、如图1,四边形为等邻边圆内接四边形, , , 直接写出的度数;(2)、如图2,四边形内接于 , 为的直径, , , 若四边形为等邻边圆内接四边形, , 求的长.(3)、如图3,四边形为等邻边圆内接四边形, , 为的直径,且.设 , 四边形的周长为 , 试确定与的函数关系式,并求出的最大值.25. 在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于点 , 过点 , 且顶点的坐标为. (1)、求二次函数的解析式;(2)、如图1,若点是二次函数图象上的点,且在直线的上方,连接 , .求面积的最大值及此时点的坐标;(3)、如图2,设点是抛物线对称轴上的一点,连接 , 将线段绕点逆时针旋转 , 点的对应点为 , 连接交抛物线于点 , 求点的坐标.
(1)、求二次函数的解析式;(2)、如图1,若点是二次函数图象上的点,且在直线的上方,连接 , .求面积的最大值及此时点的坐标;(3)、如图2,设点是抛物线对称轴上的一点,连接 , 将线段绕点逆时针旋转 , 点的对应点为 , 连接交抛物线于点 , 求点的坐标.